双指针
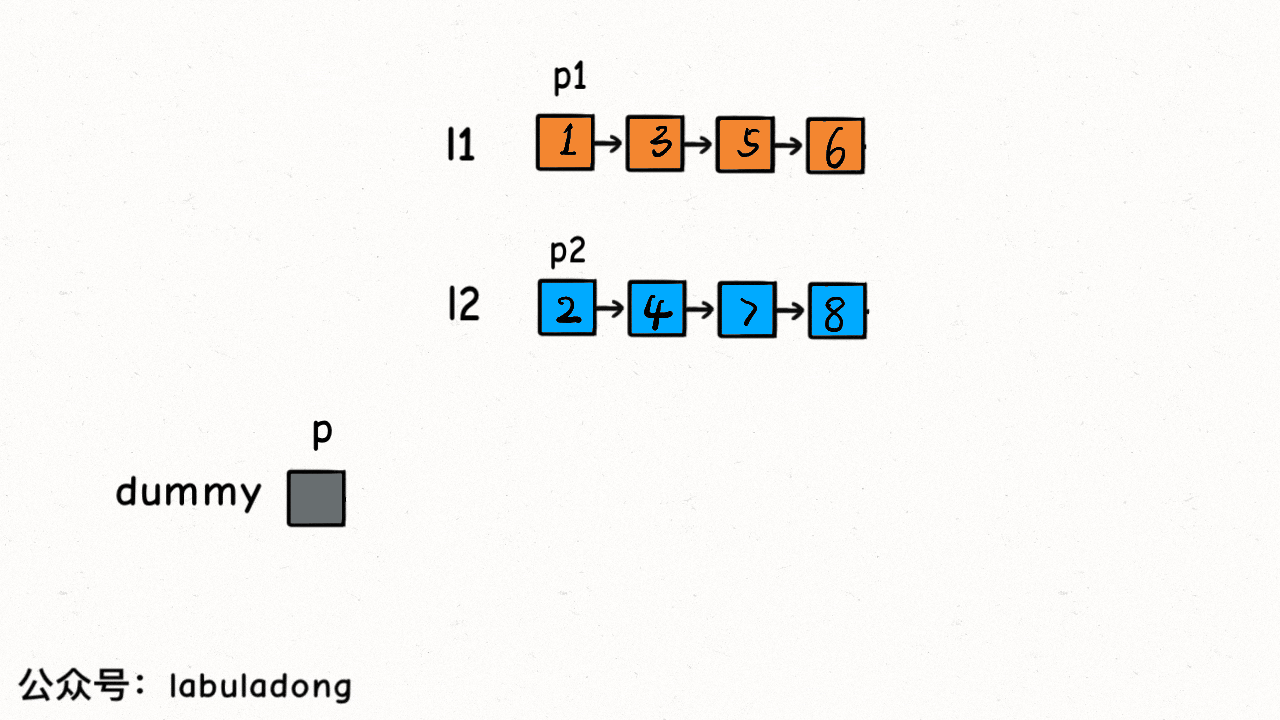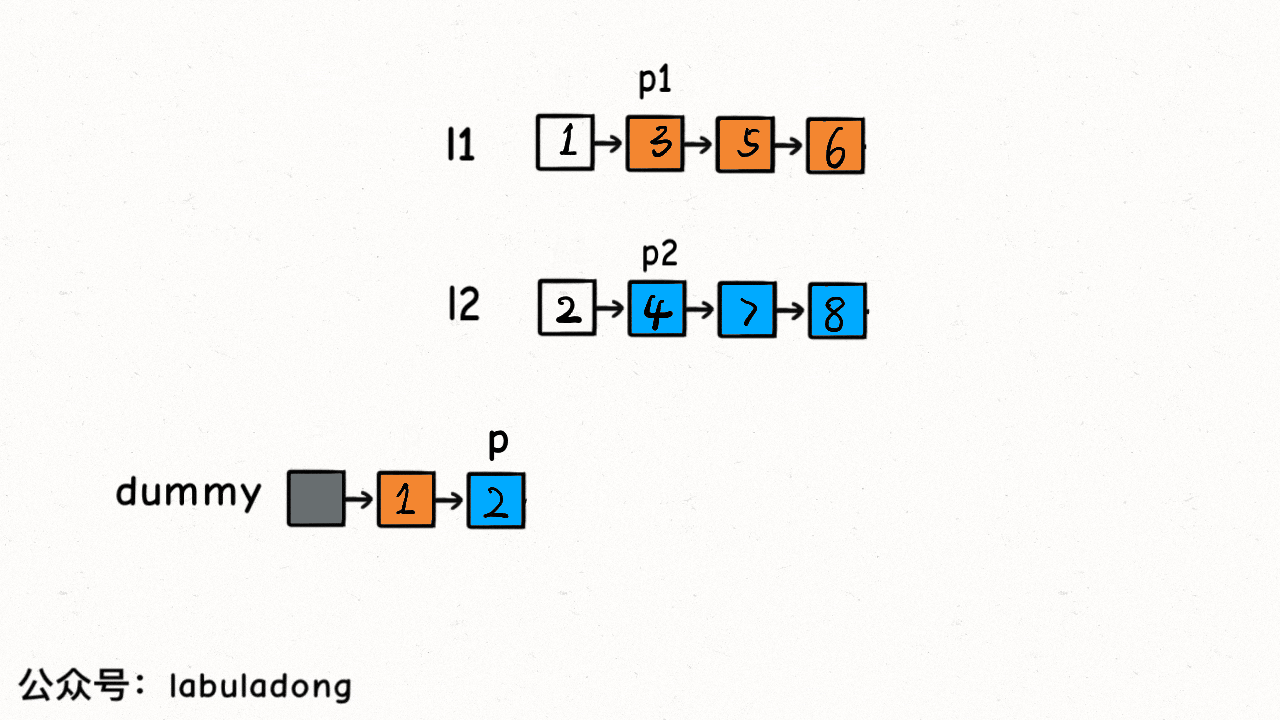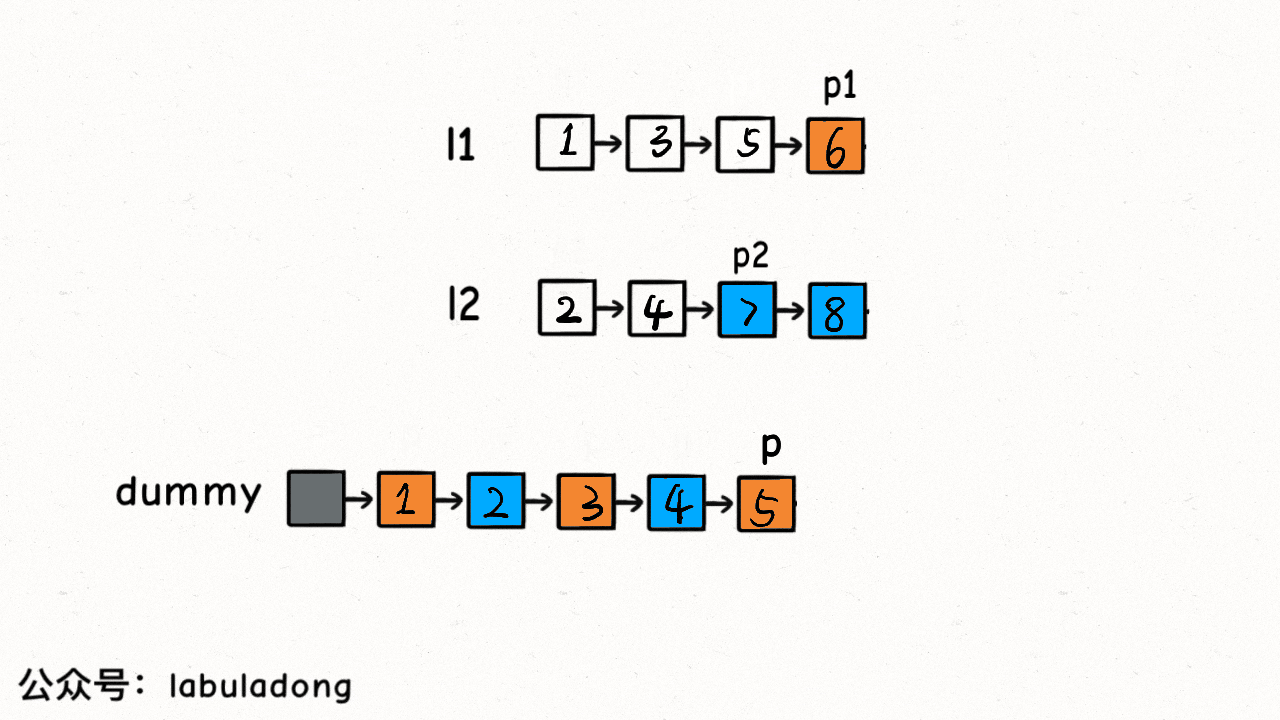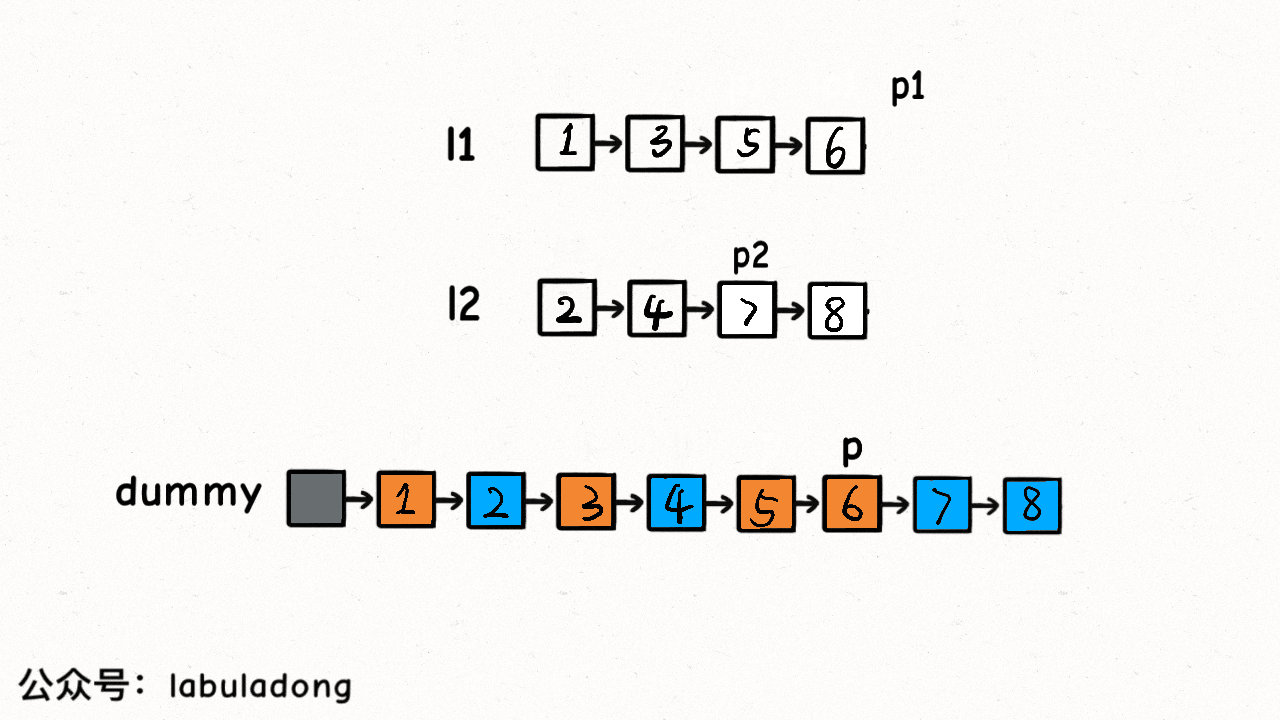
合并两个有序链表
ListNode mergeTwoLists(ListNode list1, ListNode list2) {
// 1. 定义一个虚拟头结点,作为合并链表的头结点
ListNode ret = new ListNode(-1);
// 2. 定义一个tmp结点,用于连接两个链表
ListNode tmp = ret;
// 3. 比较list1和list2的值
while (list1 != null && list2 != null) {
if (list1.val <= list2.val) {
tmp.next = list1;
list1 = list1.next;
} else {
tmp.next = list2;
list2 = list2.next;
}
tmp = tmp.next;
}
// 如果比较完成后,某个链表还有剩余,说明该链表剩余所有元素都比合并列表元素大,直接连接合并列表
if (list1 != null) {
tmp.next = list1;
}
if (list2 != null) {
tmp.next = list2;
}
return ret.next;
}
分隔链表
ListNode partition(ListNode head, int x) {
// 1. 定义两个虚拟头结点,分别作为两个分隔链表的头结点
ListNode small = new ListNode(-1), big = new ListNode(-1);
// 2. 定义两个tmp结点,用于分别连接两个分隔链表
ListNode tmpSmall = small, tmpBig = big;
// 3.1 比较head.val与x的值
while (head != null) {
if (head.val < x) {
tmpSmall.next = head;
tmpSmall = tmpSmall.next;
} else {
tmpBig.next = head;
tmpBig = tmpBig.next;
}
// 3.2 如果在这写:head = head.next; 遇到原链表是环形链表就会报错
// 因为在连接分隔链表时不只连接了一个结点,是连接了后续整个链表
// 因此应主动切断结点的后续结点,后续也应保持这个习惯!
ListNode sep = head.next;
head.next = null;
head = sep;
}
// 4. 连接两个分隔链表
tmpSmall.next = big.next;
return small.next;
}
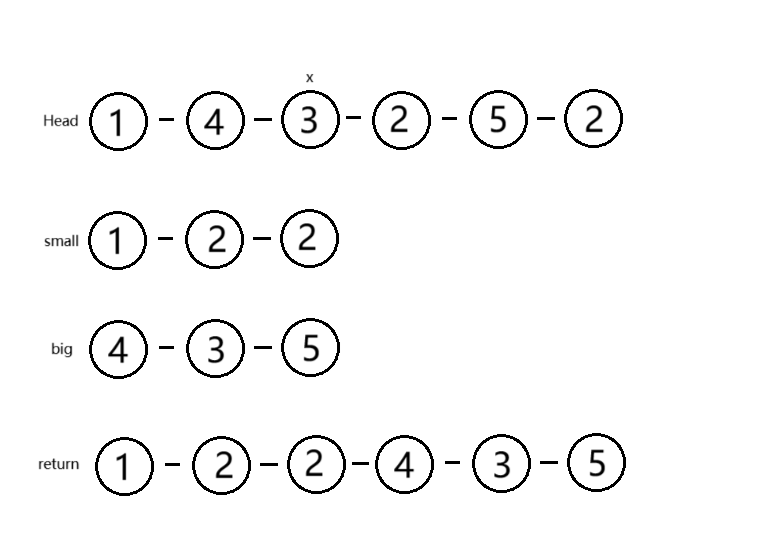
合并 K 个升序链表
ListNode mergeKLists(ListNode[] lists) {
// 特殊情况:如果传入的数组长度为0,返回空
if (lists.length == 0) {
return null;
}
// 1. 合并k个有序链表,首先应找到这k个链表的最小值。可以借助优先级队列得到最小值
PriorityQueue<ListNode> pq = new PriorityQueue<>(
lists.length, (a, b)->(a.val - b.val));
// 2.1 定义一个虚拟头结点,作为合并链表的头结点
ListNode ret = new ListNode(-1);
// 2.2 定义一个tmp结点,用于合并链表的连接
ListNode tmp = ret;
// 3. 把Listnode数组的头结点放入优先级队列中,通过堆排序得到最小值
for (ListNode head : lists) {
if (head != null) {
pq.add(head);
}
}
// 4. 连接合并链表
while (!pq.isEmpty()) {
// 4.1 将最小链表连接至合并链表
ListNode node = pq.poll();
tmp.next = node;
// 4.2 最小头结点已经被拿走,便判断该node链表是否有下一结点
// 如果有,那么把下一节点作为头结点放入优先级队列中
// 通过补充结点的操作,可以实现对所有结点的遍历
if (node.next != null) {
pq.add(node.next);
}
tmp = tmp.next;
}
return ret.next;
}
时间复杂度说明:优先队列 pq 中的元素个数最多是 k,所以一次 poll 或者 add 方法的时间复杂度是 O(logk);所有的链表节点都会被加入和弹出 pq,所以算法整体的时间复杂度是 O(Nlogk),其中 k 是链表的条数,N 是这些链表的结点总数。
链表的中间结点
想要一次遍历就获得链表的中间结点,可采用快慢指针法:快指针的移动速度是慢指针的两倍,当快指针指向 null 时,慢指针恰好到达中间结点。
注意:当链表的结点个数为偶数时,慢指针会指向中间靠后的结点。
ListNode middleNode(ListNode head) {
// 1. 定义快慢指针
ListNode slow = head, fast = head;
// 2. 快指针的移动速度是慢指针的两倍,当快指针指向null时,慢指针到达中间结点。
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
}
return slow;
}
倒数第 k 个结点
获取倒数第 k 个结点
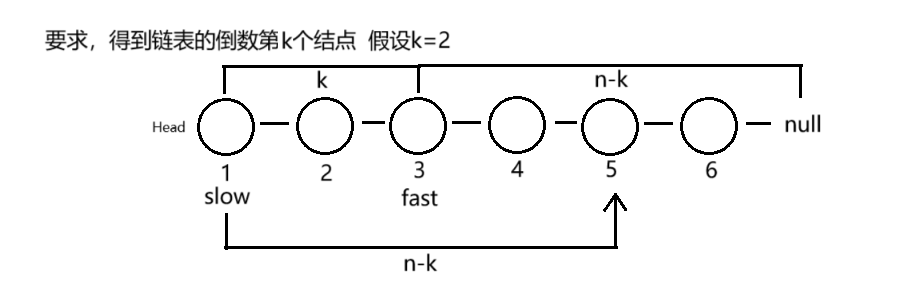
只给你一个单链表的头结点,只允许一次遍历就获得倒数第k个结点,核心思路如下:
- 先定义一个 fast 结点,先走 k 步
- 再定义一个 slow 结点,和 fast 结点同步向前走
- 当 fast == null 时,slow 结点正好走到倒数第 k 个结点
ListNode findFromEnd(ListNode head, int n) {
// 1.1 先定义一个fast结点
ListNode slow = head, fast = head;
// 1.2 让fast先走k步
while (n != 0) {
fast = fast.next;
n--;
}
// 2. 再定义一个slow结点,和fast结点一起走。
// 当fast == null时,slow结点正好走到倒数第k个结点。
while (fast != null) {
fast = fast.next;
slow = slow.next;
}
return slow;
}
删除链表的倒数第 N 个结点
如果要删除单链表的倒数第 k 个结点,核心是获取该结点的前一个结点。当 n 等于链表长度时,要删除的是头结点,直接操作会发生空指针异常,因此需要定义一个虚拟头结点,既可以避免空指针问题,又能方便地获取倒数第 k 个结点的前一个结点。
ListNode removeNthFromEnd(ListNode head, int n) {
// 1. 定义虚拟头结点
ListNode ret = new ListNode(-1);
ret.next = head;
// 2. 获得倒数第k个结点的前一节点
ListNode x = findFromEnd(ret, n + 1);
// 3. 删掉倒数第 n 个节点
x.next = x.next.next;
return ret.next;
}
ListNode findFromEnd(ListNode head, int n) {
ListNode slow = head, fast = head;
while (n != 0) {
fast = fast.next;
n--;
}
while (fast != null) {
fast = fast.next;
slow = slow.next;
}
return slow;
}
环形链表
环形链表
同样用到快慢双指针的思想:如果一个链表包含环,快指针(每次走两步)比慢指针(每次走一步)每次多走一步,最终快慢指针一定会在环内相遇;如果链表无环,快指针会先走到链表末尾(指向 null)。
boolean hasCycle(ListNode head) {
// 1. 快慢指针初始化指向 head
ListNode slow = head, fast = head;
// 2. 快指针走到末尾时停止
while (fast != null && fast.next != null) {
// 3. 慢指针走一步,快指针走两步
slow = slow.next;
fast = fast.next.next;
// 4.1 快慢指针相遇,说明含有环
if (slow == fast) {
return true;
}
}
// 4.2 能走完循环,说明不含有环
return false;
}
环形链表 II
核心推导思路:
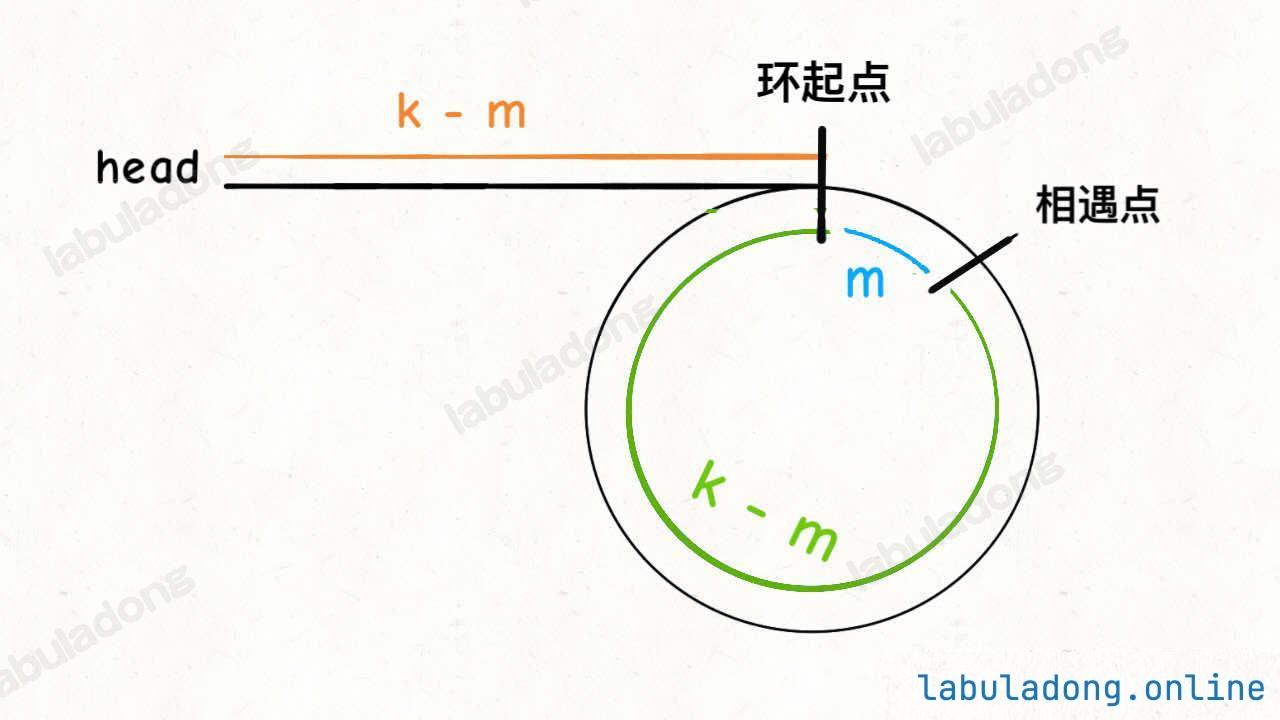
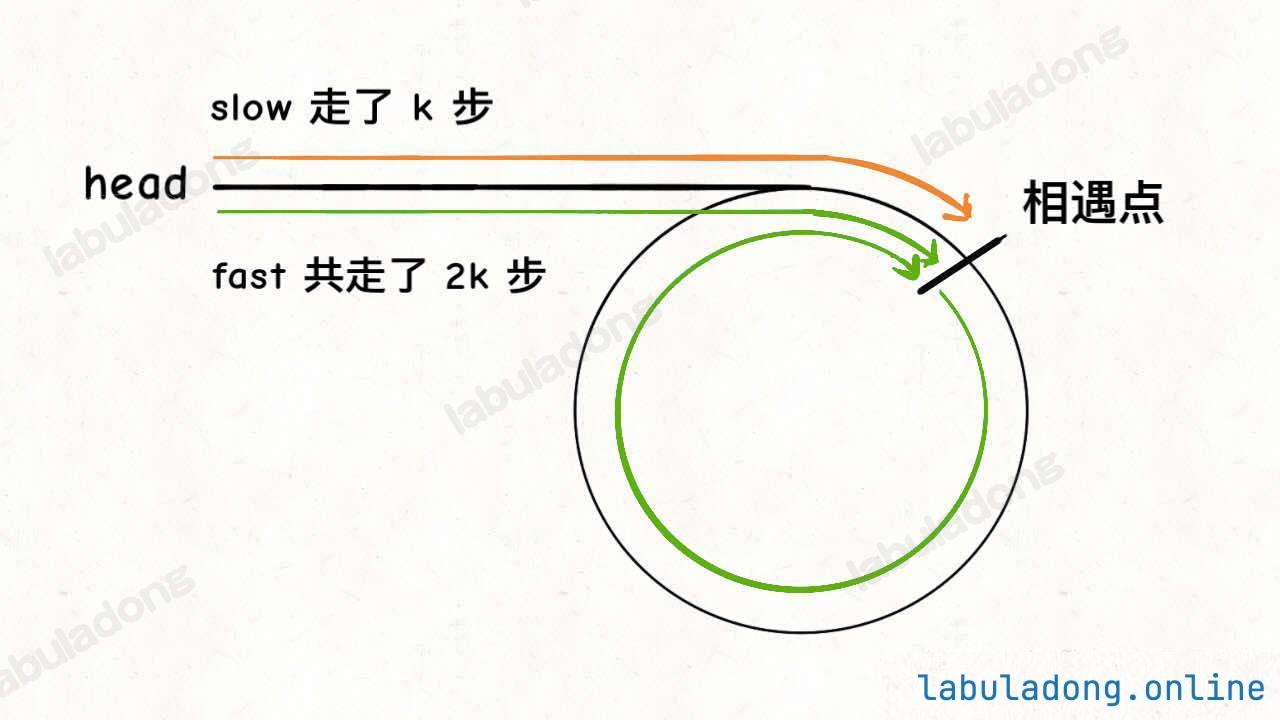
- 当快慢指针相遇时,慢指针走了 k 步,快指针走了 2k 步,多走的 k 步是在环内循环的,因此 k 是环长度的整数倍
- 设环起点到相遇点的距离为 m,则链表起点到环起点的距离为 k - m
- 相遇点到环起点的距离也为 k - m(环长度的整数倍减去 m)
- 此时将其中一个指针重置到链表起点,两个指针以相同速度前进,相遇时的结点即为环起点
ListNode detectCycle(ListNode head) {
// 1. 定义快慢结点
ListNode slow = head, fast = head;
// 2. 是否是环形链表?如果不是,返回null;如果是,双结点相遇
while (fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
if (fast == slow) {
break;
}
}
if (fast == null || fast.next == null) {
return null;
}
// 3. 寻找环起点
slow = head;
while (slow != fast) {
slow = slow.next;
fast = fast.next;
}
return slow;
}
相交链表
核心思路:拼接链表。定义两个指针分别指向两个链表的头结点,同步向前遍历,当其中一个指针走到链表末尾时,切换到另一个链表的头结点继续遍历,最终两个指针要么在相交结点相遇,要么都走到 null(无相交)。
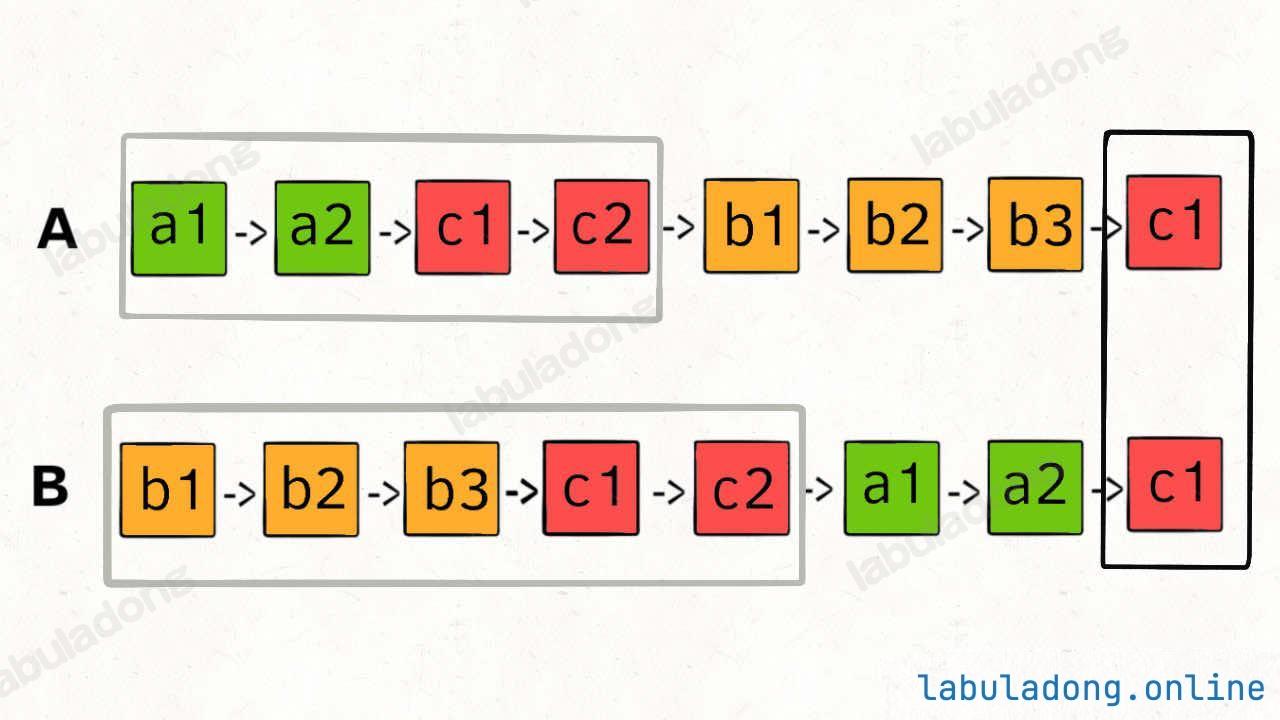
ListNode getIntersectionNode(ListNode headA, ListNode headB) {
// 1. 定义pA、pB用于拼接
ListNode pA = headA, pB = headB;
// 2. 拼接链表,两结点一致则找到交点或为空
while (pA != pB) {
// p1 走一步,如果走到 A 链表末尾,转到 B 链表
if (pA != null) {
pA = pA.next;
} else {
pA = headB;
}
// p2 走一步,如果走到 B 链表末尾,转到 A 链表
if (pB != null) {
pB = pB.next;
} else {
pB = headA;
}
}
return pA;
}
反转链表
反转链表
迭代解法
ListNode reverseList(ListNode head) {
ListNode pre = null, cur = head;
while (cur != null) {
// 在循环内定义nxt,可以省略部分代码
ListNode nxt = cur.next;
cur.next = pre;
pre = cur;
cur = nxt;
}
return pre;
}
递归解法
ListNode reverseList(ListNode head) {
// 递归终止条件:链表为空或只有一个结点
if (head == null || head.next == null) {
return head;
}
// 递归反转后续链表
ListNode newHead = reverseList(head.next);
// 调整当前结点与后续结点的指向
head.next.next = head;
head.next = null;
// 返回反转后的链表头结点
return newHead;
}
反转链表前N个结点
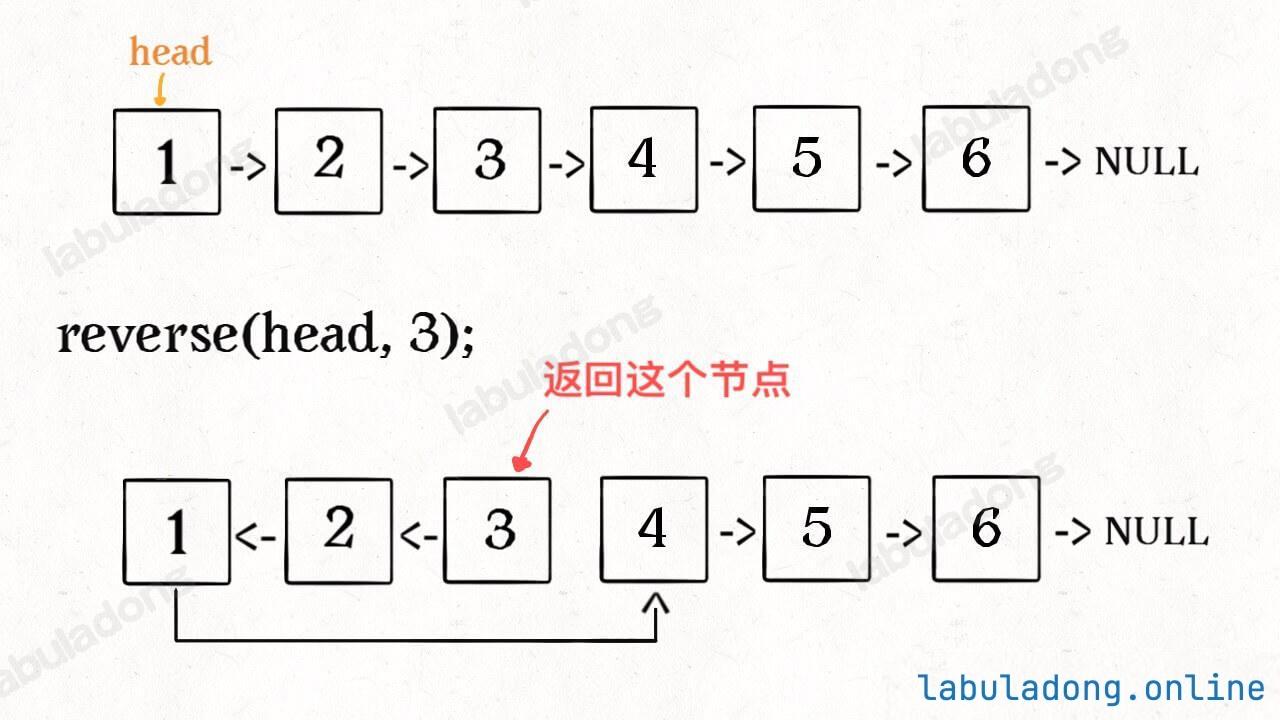
迭代解法
ListNode reverseN(ListNode head, int n) {
if (head == null || head.next == null) {
return head;
}
ListNode pre = null, cur = head;
while (n > 0) {
// 另一种写法
ListNode nxt = cur.next;
cur.next = pre;
pre = cur;
cur = nxt;
// 添加一个计数器
n--;
}
// head一直指向原链表第1个结点,在它后面连上cur结点(原第n+1个结点)即可连接整个链表
head.next = cur;
return pre;
}
递归解法
// 记录反转后第n+1个结点,用于连接原链表头部
ListNode successor = null;
ListNode reverseN(ListNode head, int n) {
// 递归终止条件:反转前1个结点,直接返回head
if (n == 1) {
// 记录第n+1个结点
successor = head.next;
return head;
}
// 递归反转前n个结点的后续部分
ListNode newHead = reverseN(head.next, n - 1);
// 调整当前结点与后续结点的指向
head.next.next = head;
// 连接反转后的链表与剩余部分
head.next = successor;
return newHead;
}
反转链表 II
迭代解法
ListNode reverseBetween(ListNode head, int m, int n) {
if (m == 1) {
return reverseN(head, n);
}
// 找到第 m 个节点的前驱
// 采用计数器的时候需谨慎!!!
ListNode pre = head;
for (int i = 1; i < m - 1; i++) {
pre = pre.next;
}
// 从第 m 个节点开始反转
pre.next = reverseN(pre.next, n - m + 1);
return head;
}
ListNode reverseN(ListNode head, int n) {
ListNode pre = null, cur = head;
while (n > 0) {
ListNode nxt = cur.next;
cur.next = pre;
pre = cur;
cur = nxt;
n--;
}
head.next = cur;
return pre;
}
K 个一组反转链表
ListNode reverseKGroup(ListNode head, int k) {
if (head == null) {
return null;
}
// 1. 找到当前组的末尾结点(第k个结点)
ListNode a = head, b = head;
for (int i = 0; i < k; i++) {
// 不足k个结点,直接返回原链表
if (b == null) {
return head;
}
b = b.next;
}
// 2. 反转当前k个结点(a到b的前一个结点)
ListNode newHead = reverse(a, b);
// 3. 递归反转后续链表,并连接当前组的末尾
a.next = reverseKGroup(b, k);
return newHead;
}
// 反转区间 [a, b) 之间的链表
ListNode reverse(ListNode a, ListNode b) {
ListNode pre = null, cur = a, nxt = a;
while (cur != b) {
nxt = cur.next;
cur.next = pre;
pre = cur;
cur = nxt;
}
// 返回反转后的头结点
return pre;
}
回文链表
回文链表
核心思路:
- 用快慢指针找到链表中点
- 反转链表的后半部分
- 对比前半部分与反转后的后半部分,判断是否为回文
- (可选)还原链表后半部分(如需保留原链表结构)
boolean isPalindrome(ListNode head) {
// 1. 找到链表中点
ListNode slow = head, fast = head;
while (fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
}
if (fast != null) { // 奇数个结点,慢指针再前进一位(跳过中间结点)
slow = slow.next;
}
// 2. 中点左边是原链表,右边是从链表尾到链表中点的反转链表
ListNode left = head;
ListNode right = reverse(slow); // 调用反转链表函数
// 3. 如果两链表值相同则为回文链表
while (right != null) {
if (left.val != right.val) {
return false;
}
left = left.next;
right = right.next;
}
return true;
}
// 反转链表(辅助函数)
ListNode reverse(ListNode head) {
ListNode pre = null, cur = head;
while (cur != null) {
ListNode next = cur.next;
cur.next = pre;
pre = cur;
cur = next;
}
return pre;
}

