一、树

树是一种非线性的数据结构。它是由 n (n >= 0) 个有限结点组成的具有层级关系的集合，不同于数组、链表这类线性结构，树的结点之间呈现出“一对多”的层级关联特性。

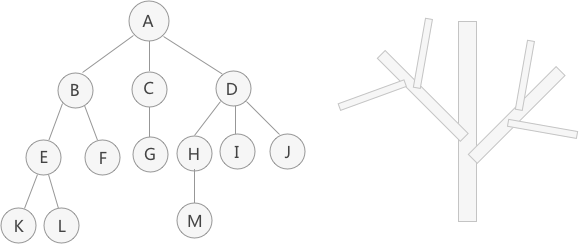
树的核心概念

在学习树结构之前，需要先掌握这些基础术语，它们是理解后续内容的前提：

结点的度：一个结点含有子树的个数称为该结点的度
树的度：一棵树中，所有结点度的最大值称为树的度
叶子结点：度为 0 的结点称为叶结点（也叫终端结点）
双亲结点/父节点：若一个结点含有子结点，则称这个结点为子结点的父结点
孩子结点/子结点：一个结点含有子树的根结点称为该节点的子结点
根结点：没有双亲结点的结点，一棵树有且仅有一个根结点（n>0 时）
结点的层次：根为第一层，根的子结点为第二层，以此类推
树的高度：树中结点的最大层次（也叫树的深度）

二、二叉树

树的结构有很多种，其中二叉树是最基础、应用最广泛的一种，满足以下两个条件的树就是二叉树：

本身是有序树（结点的左右子树有明确区分，不能随意交换）；
树中包含的各个节点的度不能超过 2（即每个结点最多有 2 棵子树，分别称为左子树和右子树）

两种特殊的二叉树

二叉树中有两种特殊形态，在算法题和实际开发中出现频率极高，分别是满二叉树和完全二叉树。

满二叉树：除了叶子结点，每个结点的度都为 2，且所有叶子结点都在同一层上。

满二叉树

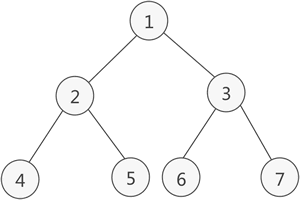
完全二叉树：除去最后一层结点为满二叉树，且最后一层的结点从左到右连续分布，没有空缺。（满二叉树是一种特殊的完全二叉树）

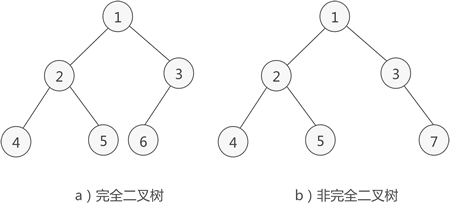
完全二叉树和非完全二叉树

二叉树的核心性质

二叉树具有一些固定的数学性质，这些性质常常作为算法题的解题突破口，需要熟练掌握：

一棵非空二叉树的第 i 层最多有 2 ^ (i - 1) 个结点（i >= 1）
深度为 k 的二叉树最多有 2 ^ k - 1 个结点（k >= 1）
对于任意一棵二叉树，若叶子结点数为 n0，度为 2 的结点数为 n2，则必有 n0 = n2 + 1
具有 n 个结点的完全二叉树深度为 ⌊log₂n⌋ + 1（或 log₂(n + 1) 向上取整）
对于具有 n 个结点的完全二叉树，若按从上至下、从左至右的顺序对所有结点从 0 开始编号，则对于序号为 i 的结点，满足以下关系：

条件	i = 0	i > 0	2i + 1 < n	2i + 2 < n
对应关系	无双亲结点	双亲序号：(i - 1) / 2（整数除法）	左孩子序号：2i + 1	右孩子序号：2i + 2

二叉树的遍历

二叉树的遍历是指按照某种规则，依次访问二叉树中的所有结点，且每个结点仅被访问一次。其中最基础的是前序、中序、后序三种深度优先遍历，它们的区别在于访问根结点的时机不同。

前序遍历：根结点 >> 左子树 >> 右子树
中序遍历：左子树 >> 根结点 >> 右子树
后序遍历：左子树 >> 右子树 >> 根结点

递归实现

递归实现是三种遍历最简洁的方式，利用了函数调用栈的特性，代码可读性极强，是日常开发和面试中的基础写法：

// 前序遍历
public void preOrder(TreeNode root) { 
    if (root == null) {
        return;
    }
    System.out.print(root.val + " "); // 先访问根结点
    preOrder(root.left); // 再递归遍历左子树
    preOrder(root.right); // 最后递归遍历右子树
}

// 中序遍历
public void inOrder(TreeNode root) { 
    if (root == null) {
        return;
    }
    inOrder(root.left); // 先递归遍历左子树
    System.out.print(root.val + " "); // 再访问根结点
    inOrder(root.right); // 最后递归遍历右子树
}

// 后序遍历
public void postOrder(TreeNode root) { 
    if (root == null) {
        return;
    }
    postOrder(root.left); // 先递归遍历左子树
    postOrder(root.right); // 再递归遍历右子树
    System.out.print(root.val + " "); // 最后访问根结点
}

迭代实现

递归实现虽然简洁，但存在栈溢出的风险（当二叉树深度过大时），此时需要用迭代方式实现，手动借助栈（Stack）数据结构来模拟递归调用栈的过程。

import java.util.Stack;

// 前序遍历迭代实现
public void preOrderIteration(TreeNode root) {
    if (root == null) {
        return;
    }
    Stack<TreeNode> stack = new Stack<>();
    stack.push(root);
    while (!stack.isEmpty()) {
        TreeNode node = stack.pop();
        System.out.print(node.val + " "); // 访问根结点
        // 栈先进后出，先压右子树，再压左子树
        if (node.right != null) {
            stack.push(node.right);
        }
        if (node.left != null) {
            stack.push(node.left);
        }
    }
}

二叉树的常用方法

在操作二叉树时，有一些高频的基础方法，同样可以用递归实现，核心思路是“分治”——将大问题拆解为左子树和右子树的小问题，再合并结果。

// 获取二叉树的结点总个数
public int size(TreeNode root) { 
    if (root == null) {
        return 0;
    }
    // 根结点个数 + 左子树结点个数 + 右子树结点个数
    return size(root.left) + size(root.right) + 1;
}

// 获取二叉树的叶子结点个数
public int getLeafNodeCount(TreeNode root) { 
    if (root == null) {
        return 0;
    }
    // 叶子结点的判断条件：左右子树都为空
    if (root.left == null && root.right == null) {
        return 1;
    }
    // 合并左、右子树的叶子结点个数
    return getLeafNodeCount(root.left) + getLeafNodeCount(root.right);
}

// 求二叉树的高度（深度）
public int getHeight(TreeNode root) { 
    if (root == null) {
        return 0;
    }
    // 二叉树高度 = 左、右子树高度的最大值 + 根结点所在层
    return Math.max(getHeight(root.left), getHeight(root.right)) + 1;
}

// 查找二叉树中是否存在指定值的结点，存在则返回该结点，否则返回null
public TreeNode find(TreeNode root, int val) { 
    if (root == null) {
        return null;
    }
    // 先判断当前根结点是否是目标结点
    if (root.val == val) {
        return root;
    }
    // 递归查找左子树
    TreeNode tmp = find(root.left, val);
    if (tmp != null) {
        return tmp;
    }
    // 左子树未找到，递归查找右子树
    tmp = find(root.right, val);
    if (tmp != null) {
        return tmp;
    }
    // 左右子树均未找到
    return null;
}

二叉树

一、树