一、链表相关算法
双指针
在链表的双指针解题中,有几个核心注意事项需要牢记:
- 计数器的使用需严谨,避免出现边界偏移
- head 结点不要随意修改,建议使用 cur 临时指针进行操作
- 如需保留原链表,要保证操作过程中不破坏原链表的结构
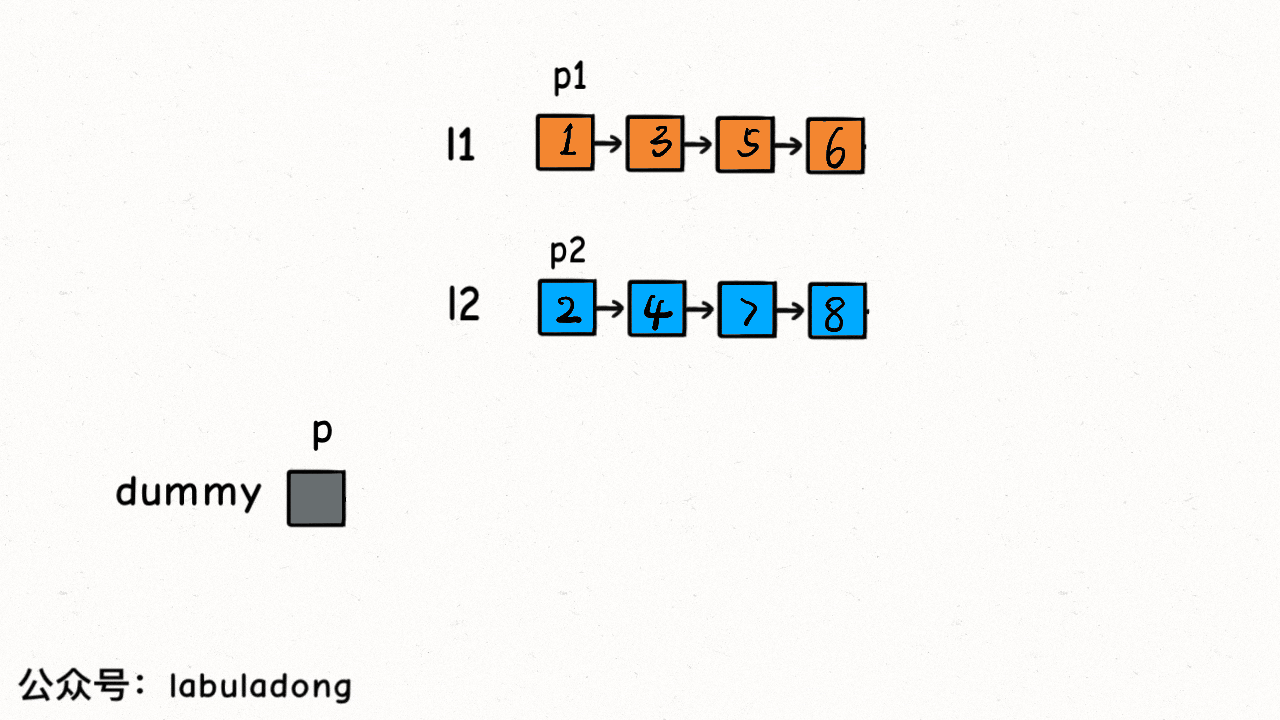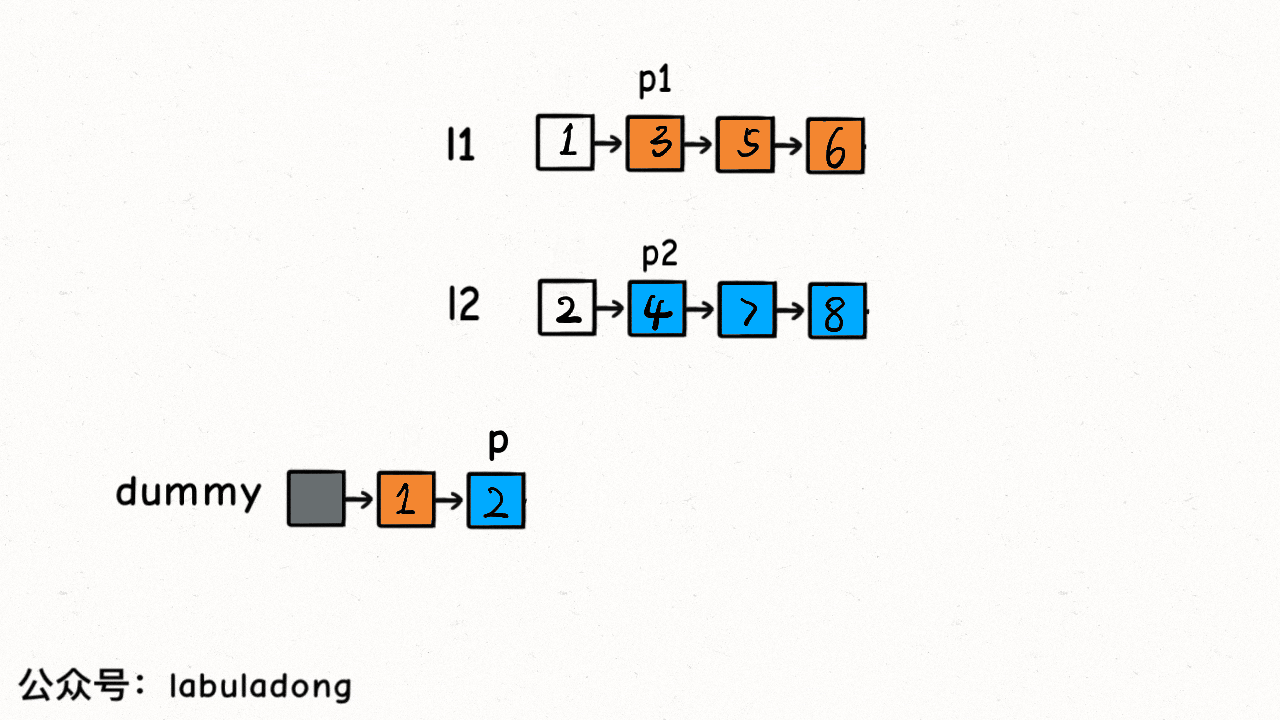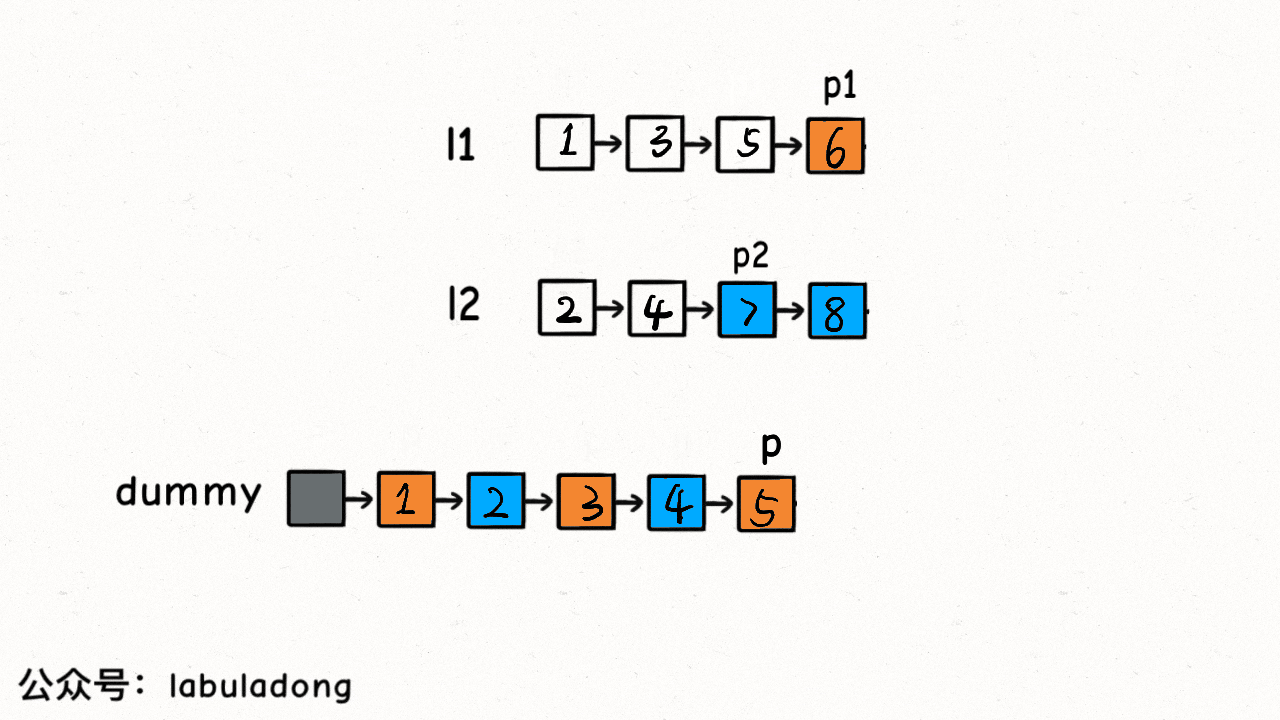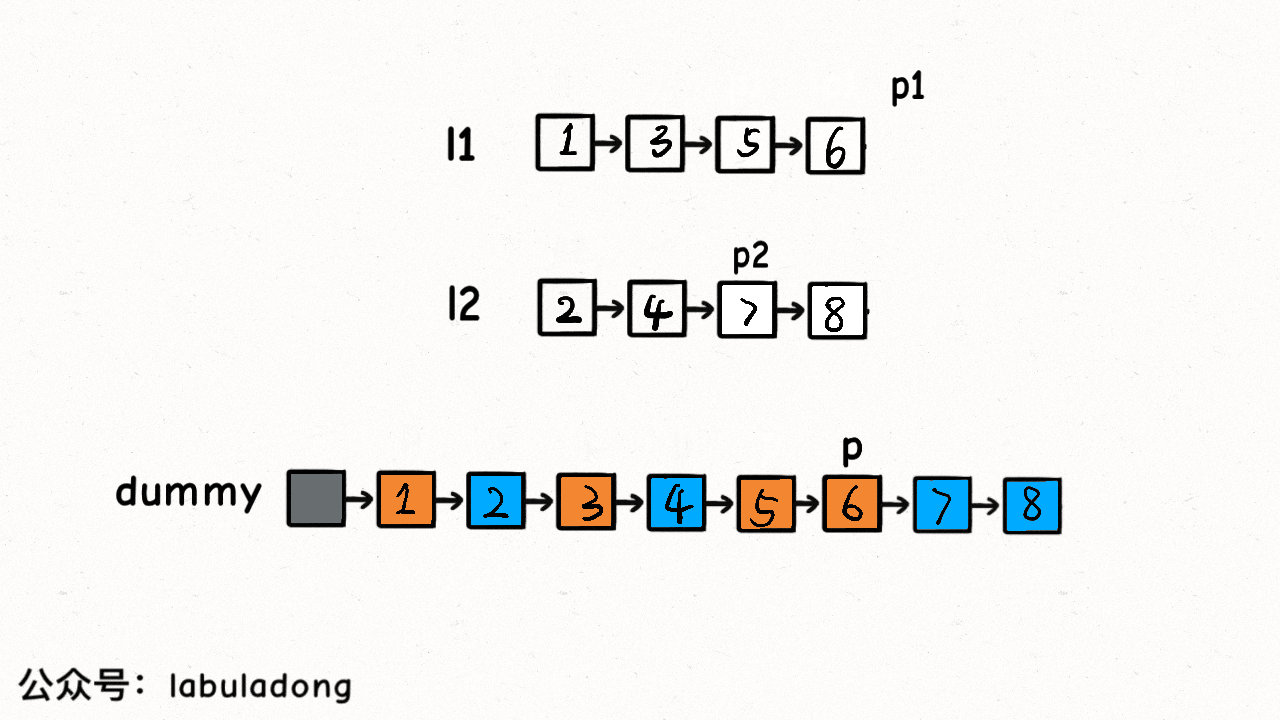
合并有序链表
ListNode mergeTwoLists(ListNode list1, ListNode list2) {
// 1. 定义一个虚拟头结点,作为合并链表的头结点
ListNode ret = new ListNode(-1);
// 2. 定义一个tmp结点,用于连接两个链表
ListNode tmp = ret;
// 3. 比较list1和list2的值
while (list1 != null && list2 != null) {
if (list1.val <= list2.val) {
tmp.next = list1;
list1 = list1.next;
} else {
tmp.next = list2;
list2 = list2.next;
}
tmp = tmp.next;
}
// 如果比较完成后,某个链表还有剩余,说明该链表剩余所有元素都比合并列表元素大,直接连接合并列表
if (list1 != null) {
tmp.next = list1;
}
if (list2 != null) {
tmp.next = list2;
}
return ret.next;
}
分隔链表
ListNode partition(ListNode head, int x) {
// 1. 定义两个虚拟头结点,分别作为两个分隔链表的头结点
ListNode small = new ListNode(-1), big = new ListNode(-1);
// 2. 定义两个tmp结点,用于分别连接两个分隔链表
ListNode tmpSmall = small, tmpBig = big;
// 3.1 比较head.val与x的值
while (head != null) {
if (head.val < x) {
tmpSmall.next = head;
tmpSmall = tmpSmall.next;
} else {
tmpBig.next = head;
tmpBig = tmpBig.next;
}
// 3.2 如果在这写:head = head.next; 遇到原链表是环形链表就会报错
// 因为在连接分隔链表时不只连接了一个结点,是连接了后续整个链表
// 因此应主动切断结点的后续结点,后续也应保持这个习惯!
ListNode sep = head.next;
head.next = null;
head = sep;
}
// 4. 连接两个分隔链表
tmpSmall.next = big.next;
return small.next;
}
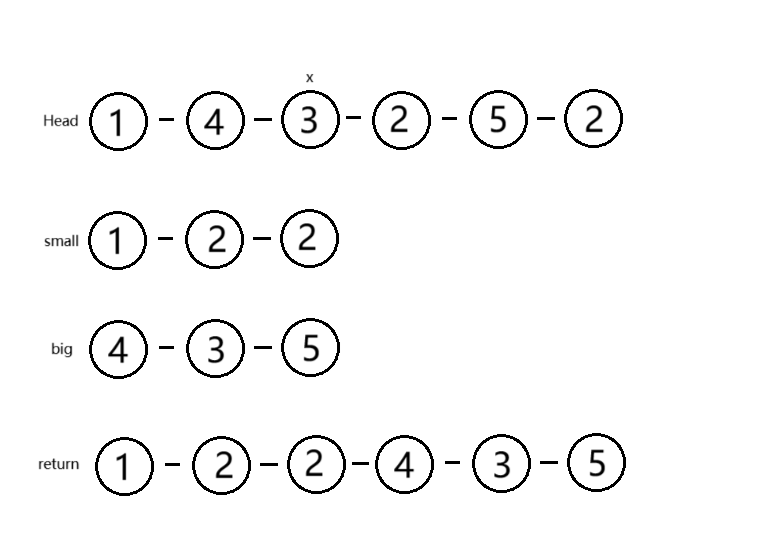
合并k个有序链表
ListNode mergeKLists(ListNode[] lists) {
// 特殊情况:如果传入的数组长度为0,返回空
if (lists.length == 0) {
return null;
}
// 1. 合并k个有序链表,首先应找到这k个链表的最小值。可以借助优先级队列得到最小值
PriorityQueue<ListNode> pq = new PriorityQueue<>(
lists.length, (a, b)->(a.val - b.val));
// 2.1 定义一个虚拟头结点,作为合并链表的头结点
ListNode ret = new ListNode(-1);
// 2.2 定义一个tmp结点,用于合并链表的连接
ListNode tmp = ret;
// 3. 把Listnode数组的头结点放入优先级队列中,通过堆排序得到最小值
for (ListNode head : lists) {
if (head != null) {
pq.add(head);
}
}
// 4. 连接合并链表
while (!pq.isEmpty()) {
// 4.1 将最小链表连接至合并链表
ListNode node = pq.poll();
tmp.next = node;
// 4.2 最小头结点已经被拿走,便判断该node链表是否有下一结点
// 如果有,那么把下一节点作为头结点放入优先级队列中
// 通过补充结点的操作,可以实现对所有结点的遍历
if (node.next != null) {
pq.add(node.next);
}
tmp = tmp.next;
}
return ret.next;
}
时间复杂度说明:优先队列 pq 中的元素个数最多是 k,所以一次 poll 或者 add 方法的时间复杂度是 O(logk);所有的链表节点都会被加入和弹出 pq,所以算法整体的时间复杂度是 O(Nlogk),其中 k 是链表的条数,N 是这些链表的结点总数。
单链表的中点
想要一次遍历就获得链表的中间结点,可采用快慢指针法:快指针的移动速度是慢指针的两倍,当快指针指向 null 时,慢指针恰好到达中间结点。
注意:当链表的结点个数为偶数时,慢指针会指向中间靠后的结点。
ListNode middleNode(ListNode head) {
// 1. 定义快慢指针
ListNode slow = head, fast = head;
// 2. 快指针的移动速度是慢指针的两倍,当快指针指向null时,慢指针到达中间结点。
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
}
return slow;
}
倒数第k个结点
获取倒数第k个结点
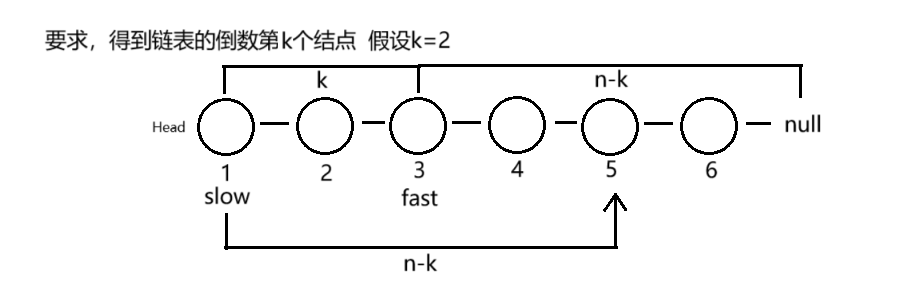
只给你一个单链表的头结点,只允许一次遍历就获得倒数第k个结点,核心思路如下:
- 先定义一个 fast 结点,先走 k 步
- 再定义一个 slow 结点,和 fast 结点同步向前走
- 当 fast == null 时,slow 结点正好走到倒数第 k 个结点
ListNode findFromEnd(ListNode head, int n) {
// 1.1 先定义一个fast结点
ListNode slow = head, fast = head;
// 1.2 让fast先走k步
while (n != 0) {
fast = fast.next;
n--;
}
// 2. 再定义一个slow结点,和fast结点一起走。
// 当fast == null时,slow结点正好走到倒数第k个结点。
while (fast != null) {
fast = fast.next;
slow = slow.next;
}
return slow;
}
删除倒数第k个结点
如果要删除单链表的倒数第 k 个结点,核心是获取该结点的前一个结点。当 n 等于链表长度时,要删除的是头结点,直接操作会发生空指针异常,因此需要定义一个虚拟头结点,既可以避免空指针问题,又能方便地获取倒数第 k 个结点的前一个结点。
ListNode removeNthFromEnd(ListNode head, int n) {
// 1. 定义虚拟头结点
ListNode ret = new ListNode(-1);
ret.next = head;
// 2. 获得倒数第k个结点的前一节点
ListNode x = findFromEnd(ret, n + 1);
// 3. 删掉倒数第 n 个节点
x.next = x.next.next;
return ret.next;
}
ListNode findFromEnd(ListNode head, int n) {
ListNode slow = head, fast = head;
while (n != 0) {
fast = fast.next;
n--;
}
while (fast != null) {
fast = fast.next;
slow = slow.next;
}
return slow;
}
环形链表
判断链表是否包含环
同样用到快慢双指针的思想:如果一个链表包含环,快指针(每次走两步)比慢指针(每次走一步)每次多走一步,最终快慢指针一定会在环内相遇;如果链表无环,快指针会先走到链表末尾(指向 null)。
boolean hasCycle(ListNode head) {
// 1. 快慢指针初始化指向 head
ListNode slow = head, fast = head;
// 2. 快指针走到末尾时停止
while (fast != null && fast.next != null) {
// 3. 慢指针走一步,快指针走两步
slow = slow.next;
fast = fast.next.next;
// 4.1 快慢指针相遇,说明含有环
if (slow == fast) {
return true;
}
}
// 4.2 能走完循环,说明不含有环
return false;
}
返回环起点
核心推导思路:
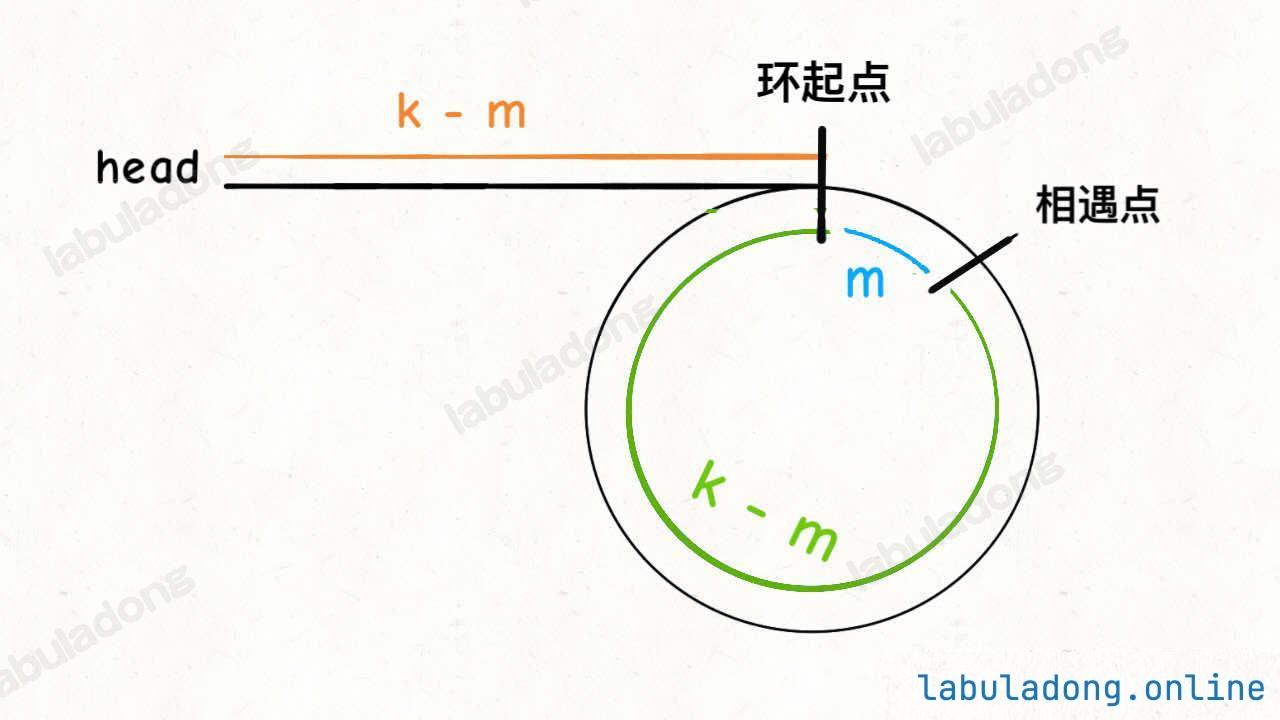
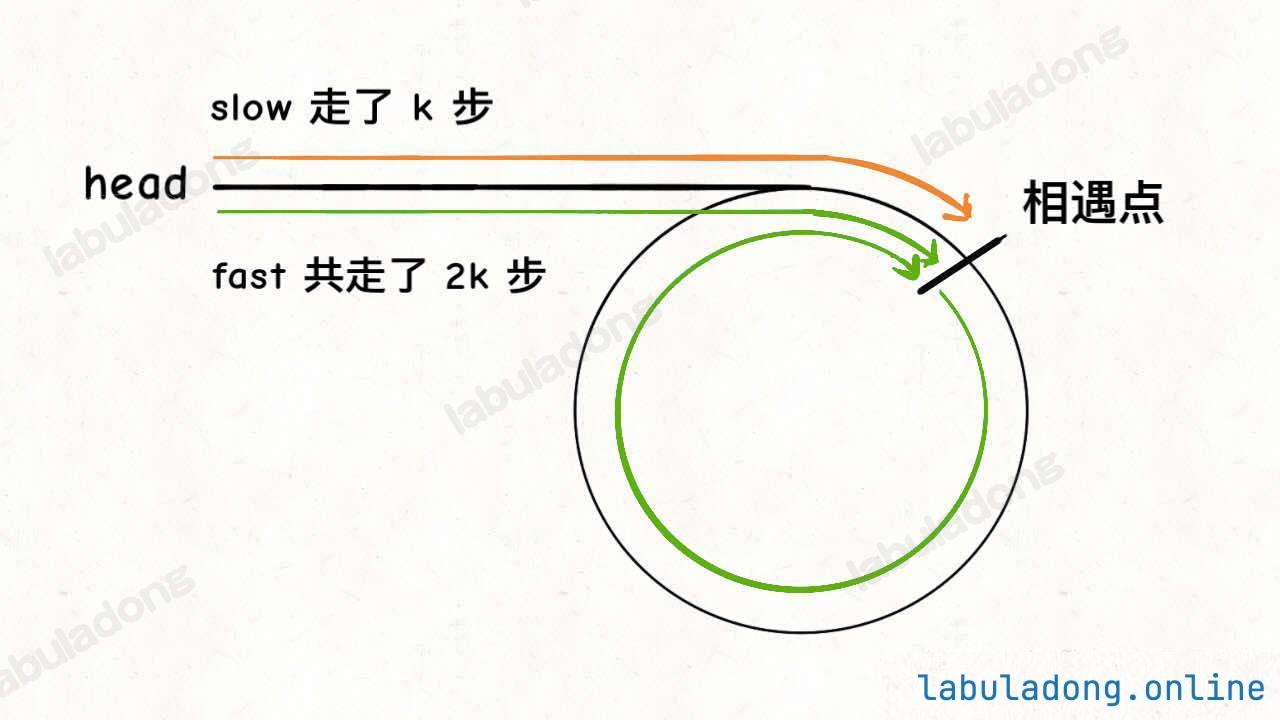
- 当快慢指针相遇时,慢指针走了 k 步,快指针走了 2k 步,多走的 k 步是在环内循环的,因此 k 是环长度的整数倍
- 设环起点到相遇点的距离为 m,则链表起点到环起点的距离为 k - m
- 相遇点到环起点的距离也为 k - m(环长度的整数倍减去 m)
- 此时将其中一个指针重置到链表起点,两个指针以相同速度前进,相遇时的结点即为环起点
ListNode detectCycle(ListNode head) {
// 1. 定义快慢结点
ListNode slow = head, fast = head;
// 2. 是否是环形链表?如果不是,返回null;如果是,双结点相遇
while (fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
if (fast == slow) {
break;
}
}
if (fast == null || fast.next == null) {
return null;
}
// 3. 寻找环起点
slow = head;
while (slow != fast) {
slow = slow.next;
fast = fast.next;
}
return slow;
}
两个链表是否相交
核心思路:拼接链表。定义两个指针分别指向两个链表的头结点,同步向前遍历,当其中一个指针走到链表末尾时,切换到另一个链表的头结点继续遍历,最终两个指针要么在相交结点相遇,要么都走到 null(无相交)。
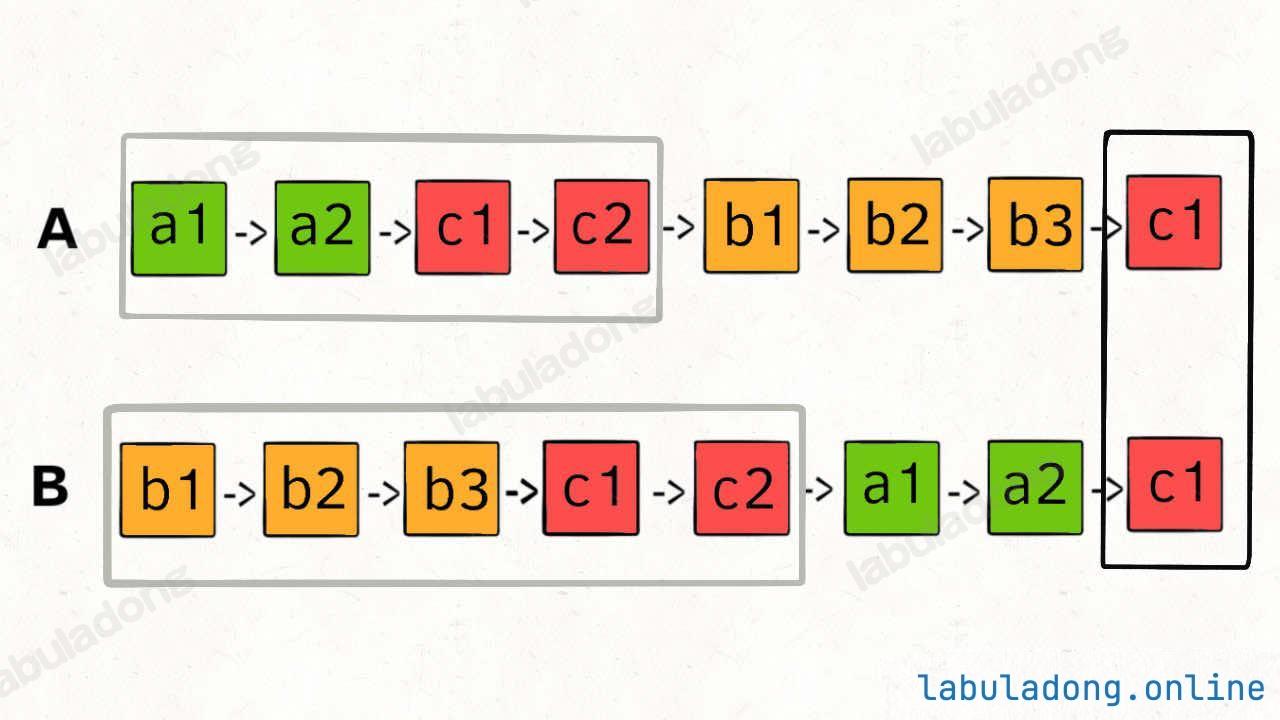
ListNode getIntersectionNode(ListNode headA, ListNode headB) {
// 1. 定义pA、pB用于拼接
ListNode pA = headA, pB = headB;
// 2. 拼接链表,两结点一致则找到交点或为空
while (pA != pB) {
// p1 走一步,如果走到 A 链表末尾,转到 B 链表
if (pA != null) {
pA = pA.next;
} else {
pA = headB;
}
// p2 走一步,如果走到 B 链表末尾,转到 A 链表
if (pB != null) {
pB = pB.next;
} else {
pB = headA;
}
}
return pA;
}
反转链表
反转整个单链表
迭代解法
ListNode reverseList(ListNode head) {
ListNode pre = null, cur = head;
while (cur != null) {
// 在循环内定义nxt,可以省略部分代码
ListNode nxt = cur.next;
cur.next = pre;
pre = cur;
cur = nxt;
}
return pre;
}
递归解法
ListNode reverseList(ListNode head) {
// 递归终止条件:链表为空或只有一个结点
if (head == null || head.next == null) {
return head;
}
// 递归反转后续链表
ListNode newHead = reverseList(head.next);
// 调整当前结点与后续结点的指向
head.next.next = head;
head.next = null;
// 返回反转后的链表头结点
return newHead;
}
反转链表前N个结点
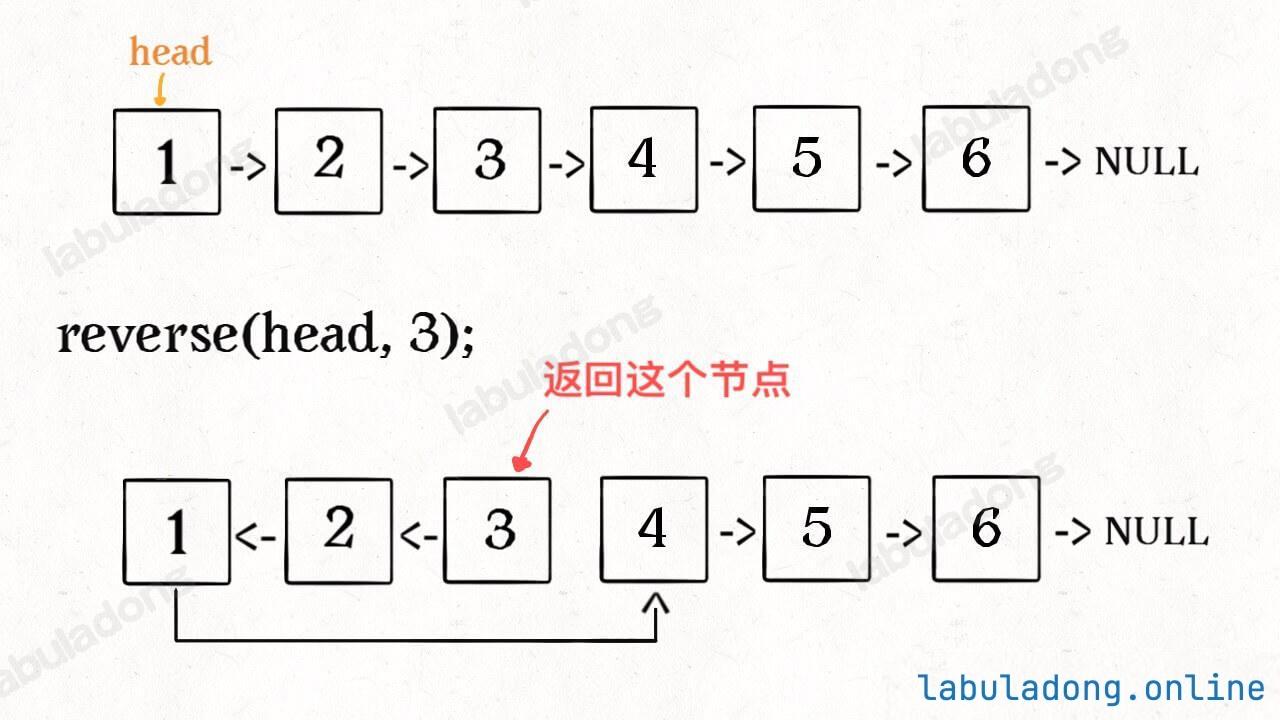
迭代解法
ListNode reverseN(ListNode head, int n) {
if (head == null || head.next == null) {
return head;
}
ListNode pre = null, cur = head;
while (n > 0) {
// 另一种写法
ListNode nxt = cur.next;
cur.next = pre;
pre = cur;
cur = nxt;
// 添加一个计数器
n--;
}
// head一直指向原链表第1个结点,在它后面连上cur结点(原第n+1个结点)即可连接整个链表
head.next = cur;
return pre;
}
递归解法
// 记录反转后第n+1个结点,用于连接原链表头部
ListNode successor = null;
ListNode reverseN(ListNode head, int n) {
// 递归终止条件:反转前1个结点,直接返回head
if (n == 1) {
// 记录第n+1个结点
successor = head.next;
return head;
}
// 递归反转前n个结点的后续部分
ListNode newHead = reverseN(head.next, n - 1);
// 调整当前结点与后续结点的指向
head.next.next = head;
// 连接反转后的链表与剩余部分
head.next = successor;
return newHead;
}
反转链表的一部分
迭代解法
ListNode reverseBetween(ListNode head, int m, int n) {
if (m == 1) {
return reverseN(head, n);
}
// 找到第 m 个节点的前驱
// 采用计数器的时候需谨慎!!!
ListNode pre = head;
for (int i = 1; i < m - 1; i++) {
pre = pre.next;
}
// 从第 m 个节点开始反转
pre.next = reverseN(pre.next, n - m + 1);
return head;
}
ListNode reverseN(ListNode head, int n) {
ListNode pre = null, cur = head;
while (n > 0) {
ListNode nxt = cur.next;
cur.next = pre;
pre = cur;
cur = nxt;
n--;
}
head.next = cur;
return pre;
}
K个一组反转链表
ListNode reverseKGroup(ListNode head, int k) {
if (head == null) {
return null;
}
// 1. 找到当前组的末尾结点(第k个结点)
ListNode a = head, b = head;
for (int i = 0; i < k; i++) {
// 不足k个结点,直接返回原链表
if (b == null) {
return head;
}
b = b.next;
}
// 2. 反转当前k个结点(a到b的前一个结点)
ListNode newHead = reverse(a, b);
// 3. 递归反转后续链表,并连接当前组的末尾
a.next = reverseKGroup(b, k);
return newHead;
}
// 反转区间 [a, b) 之间的链表
ListNode reverse(ListNode a, ListNode b) {
ListNode pre = null, cur = a, nxt = a;
while (cur != b) {
nxt = cur.next;
cur.next = pre;
pre = cur;
cur = nxt;
}
// 返回反转后的头结点
return pre;
}
回文链表
验证回文链表
核心思路:
- 用快慢指针找到链表中点
- 反转链表的后半部分
- 对比前半部分与反转后的后半部分,判断是否为回文
- (可选)还原链表后半部分(如需保留原链表结构)
boolean isPalindrome(ListNode head) {
// 1. 找到链表中点
ListNode slow = head, fast = head;
while (fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
}
if (fast != null) { // 奇数个结点,慢指针再前进一位(跳过中间结点)
slow = slow.next;
}
// 2. 中点左边是原链表,右边是从链表尾到链表中点的反转链表
ListNode left = head;
ListNode right = reverse(slow); // 调用反转链表函数
// 3. 如果两链表值相同则为回文链表
while (right != null) {
if (left.val != right.val) {
return false;
}
left = left.next;
right = right.next;
}
return true;
}
// 反转链表(辅助函数)
ListNode reverse(ListNode head) {
ListNode pre = null, cur = head;
while (cur != null) {
ListNode next = cur.next;
cur.next = pre;
pre = cur;
cur = next;
}
return pre;
}
二、顺序表相关算法
双指针
删除有序数组的重复项
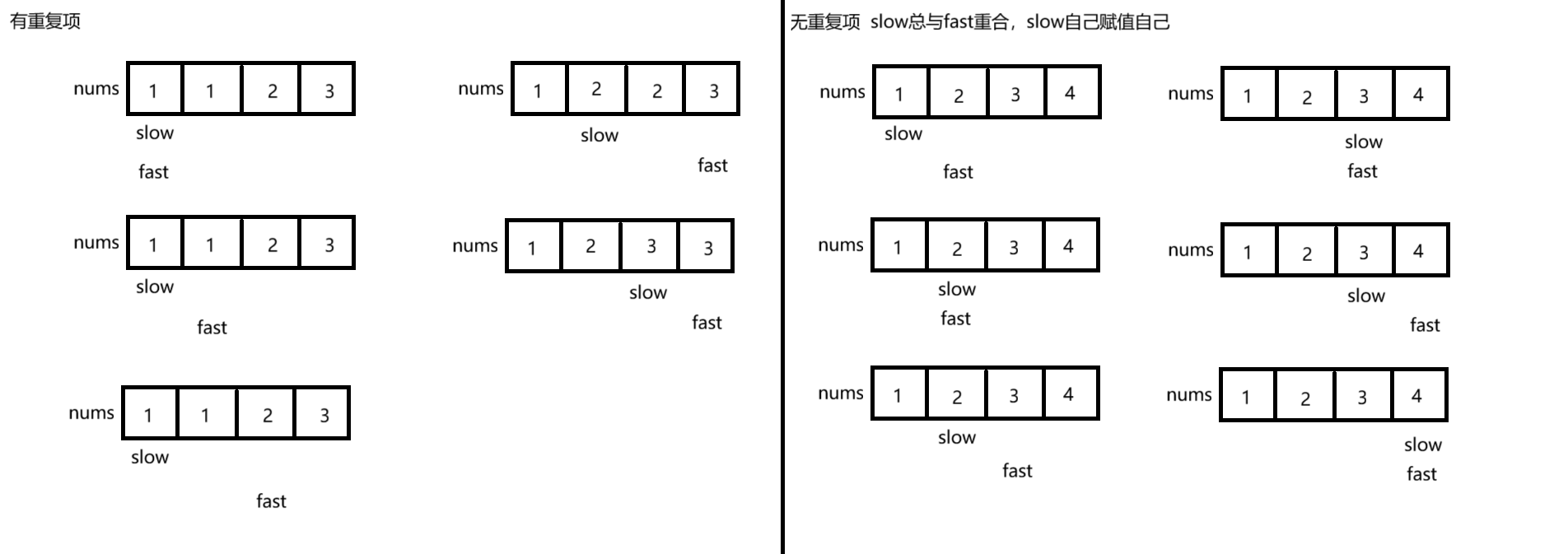
int removeDuplicates(int[] nums) {
// 特殊情况
if (nums.length == 0) {
return 0;
}
// 1. 定义快慢指针
int slow = 0, fast = 0;
// 2. 在快指针指向数组范围内操作
while (fast < nums.length) {
// 2.2 当快慢指针数字不同时,覆盖原有数字
if (nums[slow] != nums[fast]) {
slow++;
nums[slow] = nums[fast];
}
// 2.1 当nums[slow] == nums[fast]时跳到下一个
fast++;
}
// 3. 返回唯一的个数为 slow + 1
return slow + 1;
}
移除元素
int removeElement(int[] nums, int val) {
// 1. 定义快慢指针
int slow = 0, fast = 0;
// 2. 在快指针指向数组范围内操作
while (fast < nums.length) {
// 2.2 当指针数字与val不同时,覆盖数字
if (nums[fast] != val) {
nums[slow] = nums[fast];
slow++;
}
// 2.1 当nums[fast] == val的时候跳到下一个
fast++;
}
return slow;
}
移动零
void moveZeroes(int[] nums) {
// 1. 沿用上一题解,先把0全部去掉,其余顺序不变
int slow = 0, fast = 0;
while (fast < nums.length) {
if (nums[fast] != 0) {
nums[slow] = nums[fast];
slow++;
}
fast++;
}
// 2. 最后把去掉的位置都填上0
for (; slow < nums.length; slow++) {
nums[slow] = 0;
}
}
二分查找
int binarySearch(int[] nums, int target) {
// 一左一右两个指针相向而行
int left = 0, right = nums.length - 1;
while(left <= right) {
int mid = (right + left) / 2;
if(nums[mid] == target)
return mid;
else if (nums[mid] < target)
left = mid + 1;
else if (nums[mid] > target)
right = mid - 1;
}
return -1;
}
两数之和(有序数组)
LeetCode 167. 两数之和 II - 输入有序数组
int[] twoSum(int[] numbers, int target) {
// 1. 由于给定数组从下标1开始,则可以先按照正常下标运算,最后返回值+1即可
int left = 0, right = numbers.length - 1;
while (left < right) {
int sum = numbers[left] + numbers[right];
// 2.1 当和与目标数相等时,返回数组
if (sum == target) {
return new int[]{left + 1, right + 1};
}
// 2.2 当和比目标数小时,左边指针右移
else if (sum < target) {
left++;
}
// 2.3 当和比目标数大时,右边指针左移
else {
right--;
}
}
// 3. 不存在时的情况
return new int[]{-1, -1};
}
反转数组
public void reverseString(char[] s) {
int left = 0, right = s.length - 1;
while (left < right) {
char tmp = s[left];
s[left] = s[right];
s[right] = tmp;
left++;
right--;
}
}
最长回文串
String longestPalindrome(String s) {
String ret = "";
// 1. 从第一个字符开始遍历,找到最长的回文字符串
for (int i = 0; i < s.length(); i++) {
// 2.1 有两种情况,可能是偶数个,也可能是奇数个
String a = palindrome(s, i, i); // 奇数长度回文
String b = palindrome(s, i, i + 1); // 偶数长度回文
// 2.2 既是奇数偶数的长度比较,同时也是每次遍历字符串的长度比较
ret = ret.length() > a.length() ? ret : a;
ret = ret.length() > b.length() ? ret : b;
}
return ret;
}
// 寻找最长回文字符串,指针从中间开始向左右扩散
String palindrome(String s, int l, int r) {
while (l >= 0 && r < s.length() && s.charAt(l) == s.charAt(r)) {
l--;
r++;
}
// 在这里,l和r由于判断逻辑会左右多走一步
// 由于substring的范围是[left, right)
// 因此最长回文字符串是s.substring(l + 1, r)
return s.substring(l + 1, r);
}
花式遍历
旋转图像
核心技巧:顺时针旋转 = 先沿主对角线翻转矩阵 + 再沿垂直中线左右翻转,这种方法无需额外空间,效率更高。
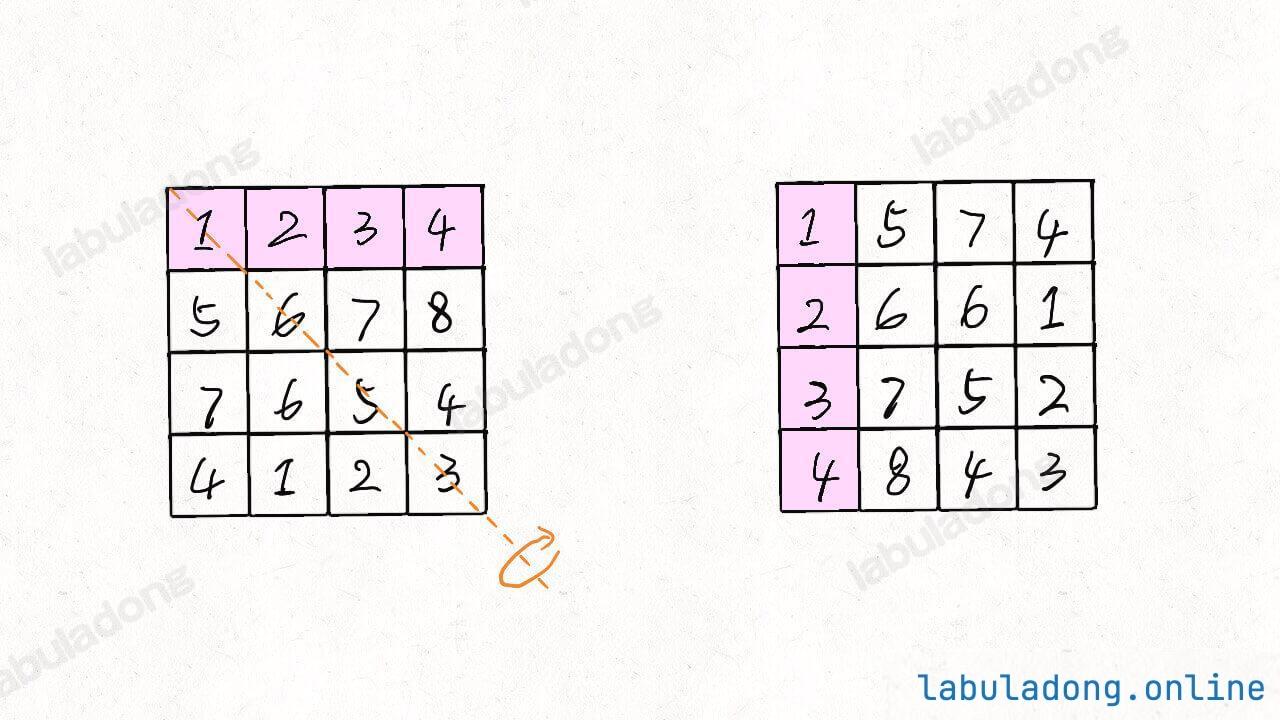
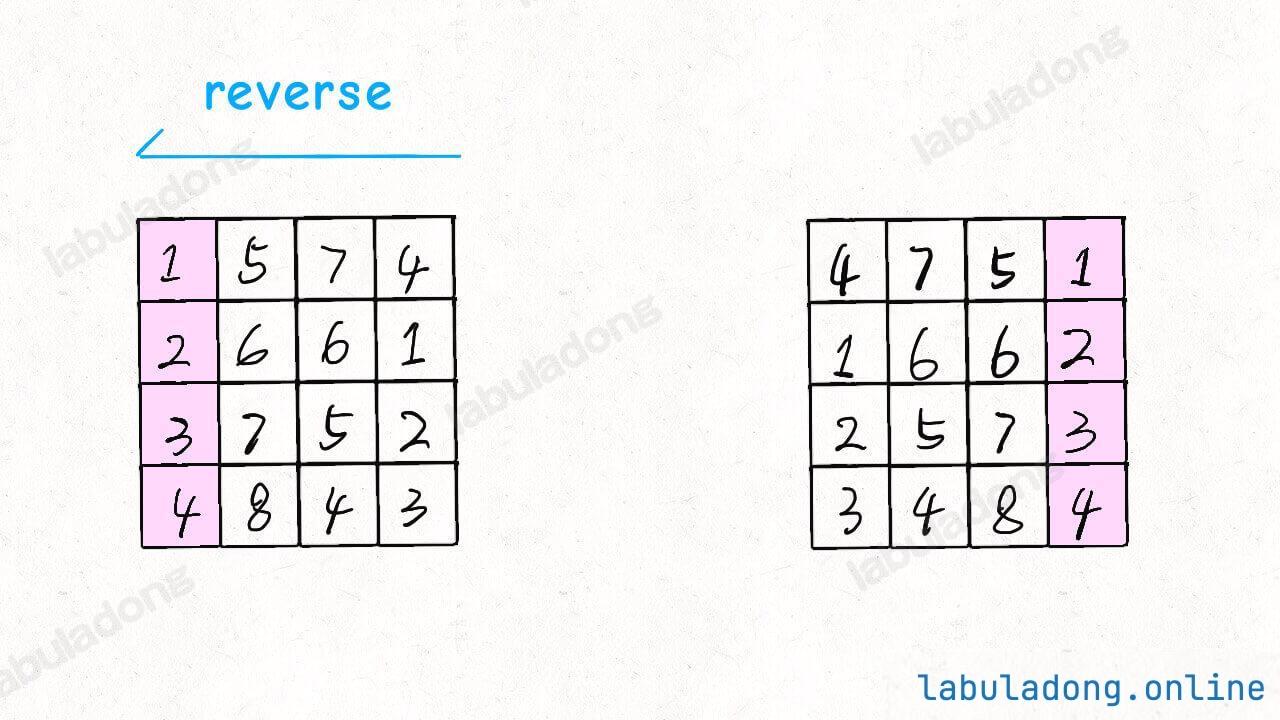
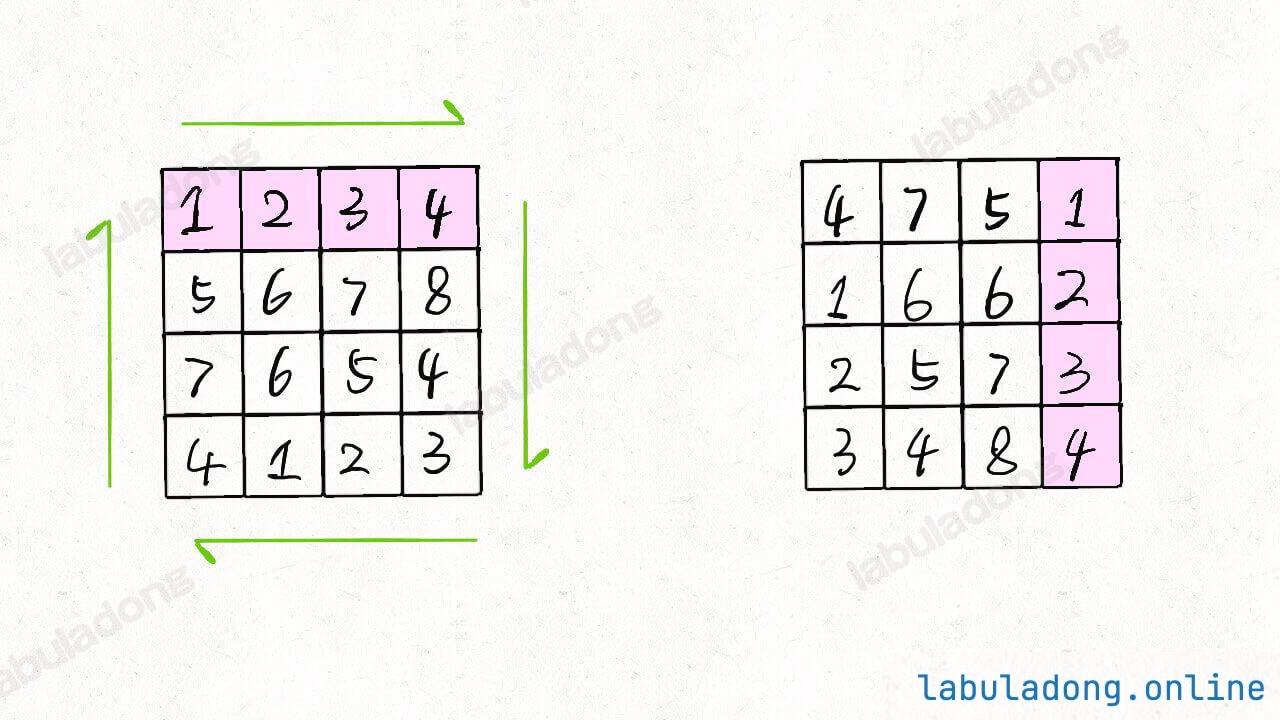
void rotate(int[][] matrix) {
// 以主对角线翻转二维数组
int n = matrix.length;
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) { // j从i开始,避免重复翻转
int tmp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = tmp;
}
}
// 左右旋转每一行数组
for (int[] arr : matrix) {
reverse(arr);
}
}
// 辅助函数:反转一维数组
void reverse(int[] arr) {
int i = 0, j = arr.length - 1;
while (i < j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
i++;
j--;
}
}
补充:逆时针旋转图像
核心技巧:逆时针旋转 = 先沿副对角线翻转矩阵 + 再沿垂直中线左右翻转。
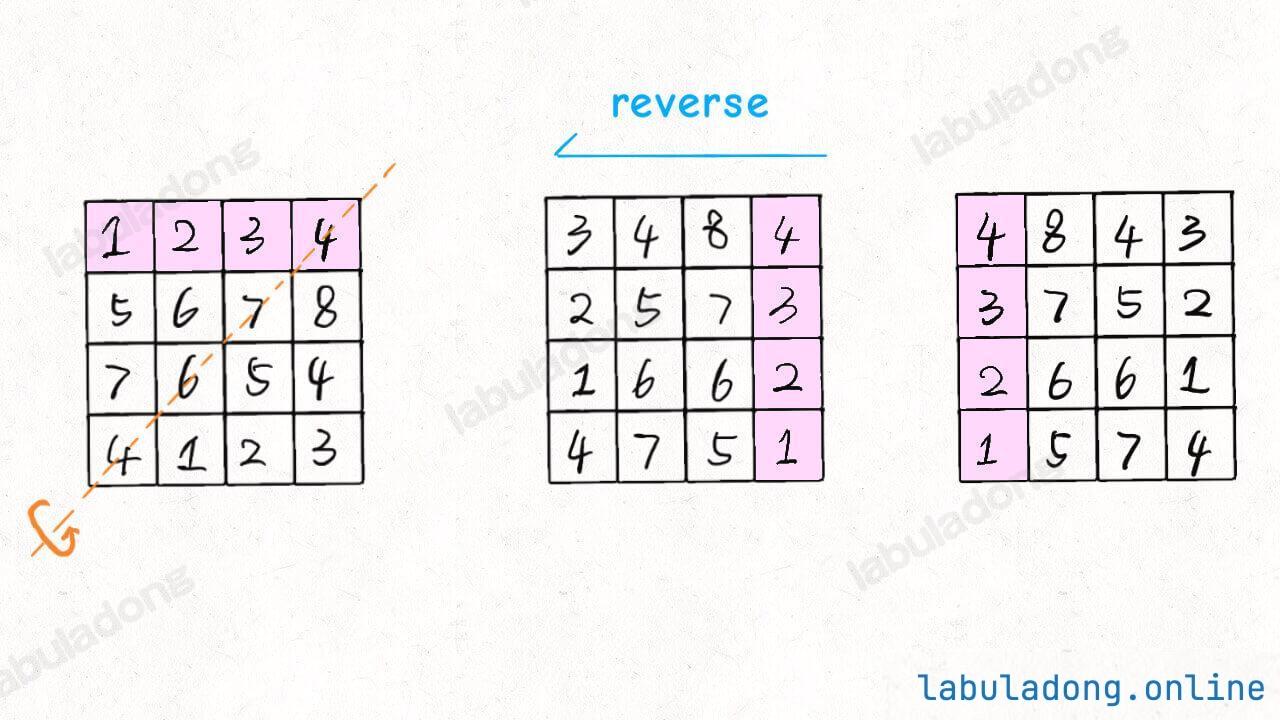
void rotate(int[][] matrix) {
int n = matrix.length;
// 沿副对角线翻转矩阵
for (int i = 0; i < n; i++) {
for (int j = n - i - 1; j >= 0; j--) {
int tmp = matrix[i][j];
matrix[i][j] = matrix[n - 1 - j][n - 1 - i];
matrix[n - 1 - j][n - 1 - i] = tmp;
}
}
// 左右旋转每一行数组
for (int[] arr : matrix) {
reverse(arr);
}
}
// 辅助函数:反转一维数组
void reverse(int[] arr) {
int i = 0, j = arr.length - 1;
while (i < j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
i++;
j--;
}
}
螺旋矩阵
核心思路:定义边界,逐步收缩。设置左、右、上、下四个边界,按照“从左到右→从上到下→从右到左→从下到上”的顺序遍历,每完成一轮遍历就收缩对应边界,直到遍历完所有元素。
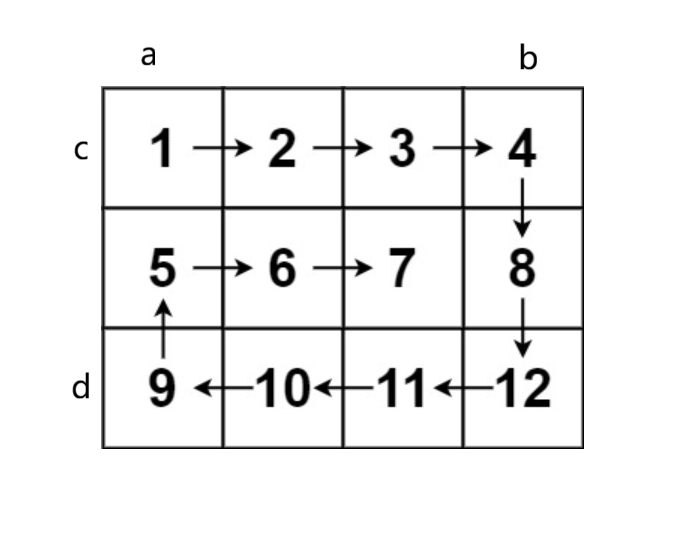
List<Integer> spiralOrder(int[][] matrix) {
int m = matrix.length, n = matrix[0].length;
int left = 0, right = n - 1; // 左右边界
int top = 0, bottom = m - 1; // 上下边界
List<Integer> list = new LinkedList<>();
while (list.size() < m * n) { // 遍历整个数组,直到收集完所有元素
// 1. 从左到右遍历上边界
if (top <= bottom) {
for (int i = left; i <= right; i++) {
list.add(matrix[top][i]);
}
top++; // 上边界下移
}
// 2. 从上到下遍历右边界
if (left <= right) {
for (int i = top; i <= bottom; i++) {
list.add(matrix[i][right]);
}
right--; // 右边界左移
}
// 3. 从右到左遍历下边界
if (top <= bottom) {
for (int i = right; i >= left; i--) {
list.add(matrix[bottom][i]);
}
bottom--; // 下边界上移
}
// 4. 从下到上遍历左边界
if (left <= right) {
for (int i = bottom; i >= top; i--) {
list.add(matrix[i][left]);
}
left++; // 左边界右移
}
}
return list;
}
nSum问题
两数之和II-输入有序数组
LeetCode 167. 两数之和 II - 输入有序数组
int[] twoSum(int[] nums, int target) {
Arrays.sort(nums);
int lo = 0, hi = nums.length - 1;
while (lo < hi) {
int sum = nums[lo] + nums[hi];
if (sum < target) {
lo++;
} else if (sum > target) {
hi--;
} else {
return new int[]{nums[lo], nums[hi]};
}
}
return new int[]{-1, -1};
}
两数之和进阶(去重)
需求:输入一个有序数组,返回所有和为 target 的不重复数对(如 nums = [1,3,1,2,2,3], target = 4,返回 [[1,3],[2,2]])。
核心难点:跳过重复元素,避免出现 [1,3] 和 [3,1]、[2,2] 和 [2,2] 这样的重复结果。
List<List<Integer>> twoSumTarget(int[] nums, int target) {
Arrays.sort(nums);
List<List<Integer>> res = new ArrayList<>();
int lo = 0, hi = nums.length - 1;
while (lo < hi) {
int sum = nums[lo] + nums[hi];
int leftVal = nums[lo], rightVal = nums[hi];
if (sum < target) {
// 跳过左侧重复元素
while (lo < hi && nums[lo] == leftVal) lo++;
} else if (sum > target) {
// 跳过右侧重复元素
while (lo < hi && nums[hi] == rightVal) hi--;
} else {
// 记录符合条件的数对
res.add(new ArrayList<>(Arrays.asList(leftVal, rightVal)));
// 跳过两侧重复元素
while (lo < hi && nums[lo] == leftVal) lo++;
while (lo < hi && nums[hi] == rightVal) hi--;
}
}
return res;
}
三数之和
核心思路:拆解问题,将三数之和拆分为“一个固定数 + 两数之和”,利用两数之和的解法完成,同时注意去重。
List<List<Integer>> threeSum(int[] nums, int target) {
Arrays.sort(nums);
List<List<Integer>> ret = new ArrayList<>();
// 1. 遍历固定第一个数
for (int i = 0; i < nums.length; i++) {
// 调用两数之和解法,寻找和为 target - nums[i] 的数对
List<List<Integer>> tmp = twoSumTarget(nums, i + 1, target - nums[i]);
for (List<Integer> tuple : tmp) {
// 2. 组合三数并加入结果集
tuple.add(nums[i]);
ret.add(tuple);
}
// 3. 跳过第一个数的重复元素,避免重复结果
while (i < nums.length - 1 && nums[i] == nums[i + 1]) i++;
}
return ret;
}
// 两数之和(带起始下标,去重)
List<List<Integer>> twoSumTarget(int[] nums, int start, int target) {
List<List<Integer>> ret = new ArrayList<>();
int lo = start, hi = nums.length - 1;
while (lo < hi) {
int sum = nums[lo] + nums[hi];
int leftVal = nums[lo], rightVal = nums[hi];
if (sum < target) {
while (lo < hi && nums[lo] == leftVal) lo++;
} else if (sum > target) {
while (lo < hi && nums[hi] == rightVal) hi--;
} else {
ret.add(new ArrayList<>(Arrays.asList(leftVal, rightVal)));
while (lo < hi && nums[lo] == leftVal) lo++;
while (lo < hi && nums[hi] == rightVal) hi--;
}
}
return ret;
}
四数之和
核心思路:递归拆解,将四数之和拆分为“一个固定数 + 三数之和”,再将三数之和拆分为“一个固定数 + 两数之和”,逐层解决,同时注意处理数值溢出问题。
public List<List<Integer>> fourSum(int[] nums, int target) {
Arrays.sort(nums);
List<List<Integer>> ret = new ArrayList<>();
// 1. 遍历固定第一个数
for (int i = 0; i < nums.length; i++) {
// 调用三数之和解法,寻找和为 target - nums[i] 的三元组
List<List<Integer>> tmp = threeSumTarget(nums, i + 1, (long) target - nums[i]);
for (List<Integer> tuple : tmp) {
// 2. 组合四数并加入结果集
tuple.add(nums[i]);
ret.add(tuple);
}
// 3. 跳过第一个数的重复元素,避免重复结果
while (i < nums.length - 1 && nums[i] == nums[i + 1]) i++;
}
return ret;
}
// 三数之和(带起始下标,处理溢出)
List<List<Integer>> threeSumTarget(int[] nums,int start, long target) {
List<List<Integer>> ret = new ArrayList<>();
// 1. 遍历固定第二个数
for (int i = start; i < nums.length; i++) {
// 调用两数之和解法,寻找和为 target - nums[i] 的数对
List<List<Integer>> tmp = twoSumTarget(nums, i + 1, target - nums[i]);
for (List<Integer> tuple : tmp) {
// 2. 组合三数并加入结果集
tuple.add(nums[i]);
ret.add(tuple);
}
// 3. 跳过第二个数的重复元素,避免重复结果
while (i < nums.length - 1 && nums[i] == nums[i + 1]) i++;
}
return ret;
}
// 两数之和(带起始下标,处理溢出)
List<List<Integer>> twoSumTarget(int[] nums, int start, long target) {
List<List<Integer>> ret = new ArrayList<>();
int lo = start, hi = nums.length - 1;
while (lo < hi) {
long sum = (long) nums[lo] + nums[hi];
int leftVal = nums[lo], rightVal = nums[hi];
if (sum < target) {
while (lo < hi && nums[lo] == leftVal) lo++;
} else if (sum > target) {
while (lo < hi && nums[hi] == rightVal) hi--;
} else {
ret.add(new ArrayList<>(Arrays.asList(leftVal, rightVal)));
while (lo < hi && nums[lo] == leftVal) lo++;
while (lo < hi && nums[hi] == rightVal) hi--;
}
}
return ret;
}
前缀和
区域和检索-数组不可变
普通解法(效率较低)
如果不使用前缀和,每次查询都需要遍历区间求和,sumRange() 方法的时间复杂度为 O(N),多次查询时性能开销过大。
class NumArray {
private int[] nums;
public NumArray(int[] nums) {
this.nums = nums;
}
int sumRange(int left, int right) {
int sum = 0;
for (int i = left; i <= right; i++) {
sum += nums[i];
}
return sum;
}
}
前缀和解法(高效优化)
核心思路:预处理前缀和数组,提前计算从数组起始位置到每个下标位置的元素和,查询时只需通过前缀和数组的差值快速得到区间和,sumRange() 方法的时间复杂度优化为 O(1)。
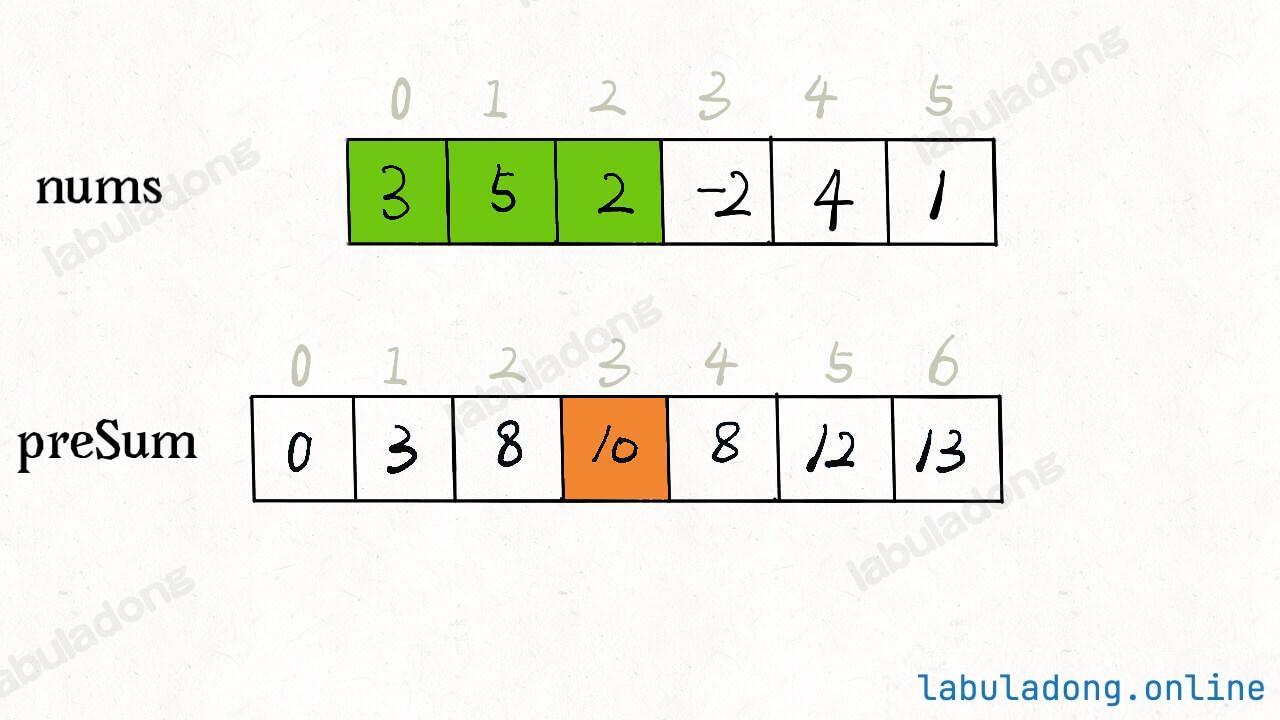
class NumArray {
int[] preSum; // 前缀和数组:preSum[i] 表示 nums[0..i-1] 的元素和
public NumArray(int[] nums) {
preSum = new int[nums.length + 1];
// 构建前缀和数组
for (int i = 1; i < preSum.length; i++) {
preSum[i] = preSum[i - 1] + nums[i - 1];
}
}
// 查询 [left, right] 区间的元素和
public int sumRange(int left, int right) {
return preSum[right + 1] - preSum[left];
}
}
二维区域和检索-矩阵不可变
核心思路:预处理二维前缀和数组,任意子矩阵的元素和可以通过二维前缀和数组的四个角点差值计算得到,避免重复遍历子矩阵。
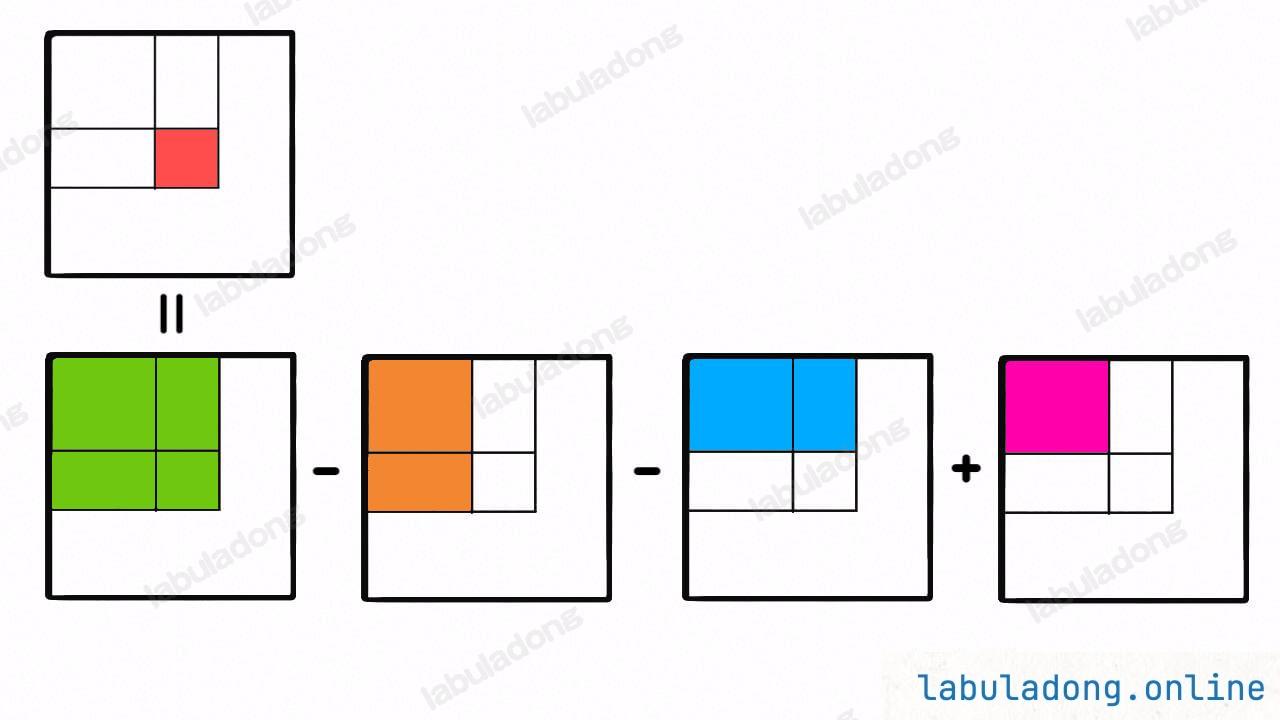
class NumMatrix {
int[][] preSum; // 二维前缀和数组:preSum[i][j] 表示矩阵 [0..i-1][0..j-1] 的元素和
public NumMatrix(int[][] matrix) {
if (matrix.length == 0 || matrix[0].length == 0) {
preSum = new int[0][0];
return;
}
int m = matrix.length, n = matrix[0].length;
preSum = new int[m + 1][n + 1];
// 构建二维前缀和数组
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
preSum[i][j] = preSum[i - 1][j] + preSum[i][j - 1] - preSum[i - 1][j - 1] + matrix[i - 1][j - 1];
}
}
}
// 查询子矩阵 [row1, col1] 到 [row2, col2] 的元素和
public int sumRegion(int row1, int col1, int row2, int col2) {
return preSum[row2 + 1][col2 + 1] - preSum[row1][col2 + 1] - preSum[row2 + 1][col1] + preSum[row1][col1];
}
}

